题目内容
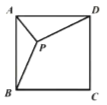
【题目】正方形![]() 的边长为4,
的边长为4,![]() 为正方形内任意一点,连接
为正方形内任意一点,连接![]() 、
、![]() 、
、![]() ,
,![]() 的最小值为____________.
的最小值为____________.
【答案】![]()
【解析】
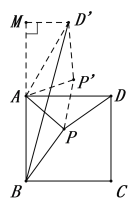
顺时针旋转△APD,可得△PAP为等边三角形,即得PA+PB+PD=PB+PP+PD,所以只要点B、P、P、D在同一条直线上时,PB+PP+PD值最小,最小值为线段BD长,根据勾股定理求线段BD长.
解:如图,以A为中心,逆时针旋转△APD至△APD,则△PAP为等边三角形,则PA+PB+PD=PB+PP+PD,
∴当点B、P、P、D在同一条直线上时,PB+PP+PD值最小,最小值为线段BD长.
作直线DM⊥AB交BA延长线于M点,
∵AD=AD=4,∠DAM=30°,
∴DM=2,
∴根据勾股定理得,AM=![]() ,
,
∴BM=4+![]() ,
,
∴根据勾股定理得,
BD=![]()
=![]()
=![]() .
.
∴![]() 的最小值为
的最小值为![]() .
.
故答案为:![]()

练习册系列答案
相关题目