题目内容
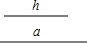用尺规作图“已知底边和底边上的高线，作等腰三角形”，有下列作法：
①作线段BC=a；
②作线段BC的垂直平分线m，交BC于点D；
③在直线m上截取DA=h，连接AB、AC．
这样作法的根据是
- A.等腰三角形三线合一
- B.等腰三角形两底角相等
- C.等腰三角形两腰相等
- D.等腰三角形的轴对称性
A
分析：根据作法可知是作出等腰三角形底边的垂直平分线，根据等腰三角形三线合一的性质即可作出选择．
解答：由分析可知，已知底边和底边上的高线，作等腰三角形的作法符合等腰三角形三线合一的性质．
故选A．
点评：考查了等腰三角形的性质：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
分析：根据作法可知是作出等腰三角形底边的垂直平分线，根据等腰三角形三线合一的性质即可作出选择．
解答：由分析可知，已知底边和底边上的高线，作等腰三角形的作法符合等腰三角形三线合一的性质．
故选A．
点评：考查了等腰三角形的性质：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
练习册系列答案
优等生题库系列答案
相关题目
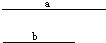
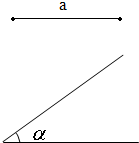19、作图：请你作出一个以线段a为底边，以∠α为底角的等腰三角形（要求：用尺规作图，并写出已知，求作，保留作图痕迹，不写作法和结论）
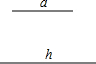（1）画一个等腰△ABC，使底边长BC为a，BC上的高为h（要求：用尺规作图，保留作图痕迹，写出已知）；