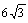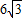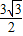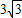题目内容
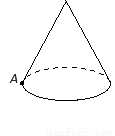
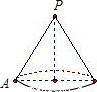
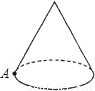
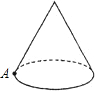 如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是( )
如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是( )A、6
| ||||
B、
| ||||
C、3
| ||||
| D、3 |
分析:圆锥的侧面展开图是扇形,从A点出发绕侧面一周,再回到A点的最短的路线即展开得到的扇形的弧所对直径,转化为求直径的长的问题.
解答: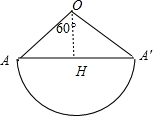 解:∵图扇形的弧长是2π,根据弧长公式得到2π=
解:∵图扇形的弧长是2π,根据弧长公式得到2π=
,
∴n=120°即扇形的圆心角是120°,
∴弧所对的弦长AA′=2×3sin60°=3
,
故选C.
 解:∵图扇形的弧长是2π,根据弧长公式得到2π=
解:∵图扇形的弧长是2π,根据弧长公式得到2π=| 3πn |
| 180 |
∴n=120°即扇形的圆心角是120°,
∴弧所对的弦长AA′=2×3sin60°=3
| 3 |
故选C.
点评:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
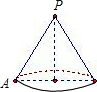 如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是
如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是