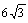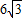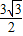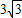题目内容
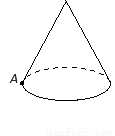
如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是 .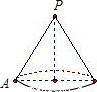
【答案】分析:圆锥的侧面展开图是扇形,从A点出发绕侧面一周,再回到A点的最短的路线即展开得到的扇形的弧所对弦,转化为求弦的长的问题.
解答: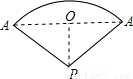 解:∵图中扇形的弧长是2π,根据弧长公式得到2π=
解:∵图中扇形的弧长是2π,根据弧长公式得到2π=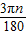
∴n=120°即扇形的圆心角是120°
∴弧所对的弦长是2×3sin60°=3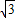
点评:正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
解答:
 解:∵图中扇形的弧长是2π,根据弧长公式得到2π=
解:∵图中扇形的弧长是2π,根据弧长公式得到2π=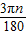
∴n=120°即扇形的圆心角是120°
∴弧所对的弦长是2×3sin60°=3
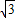
点评:正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
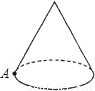
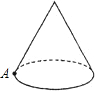 如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是( )
如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是( )A、6
| ||||
B、
| ||||
C、3
| ||||
| D、3 |
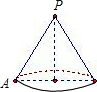 如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是
如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A点的最短的路线长是