题目内容
(2012•浙江一模)如图1,在平面上,给定了半径为r的⊙O,对于任意点P,在射线OP上取一点P′,使得OP•OP′=r2,这种把点P变为点P′的变换叫做反演变换,点P与点P′叫做互为反演点,⊙O称为基圆.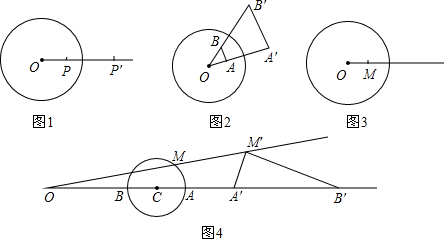
(1)如图2,⊙O内有不同的两点A、B,它们的反演点分别是A′、B′,则与∠A′一定相等的角是
(A)∠O (B)∠OAB (C)∠OBA (D)∠B′
(2)如图3,⊙O内有一点M,请用尺规作图画出点M的反演点M′;(保留画图痕迹,不必写画法).
(3)如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆O的半径为r,另一个半径为r1的⊙C,作射线OC交⊙C于点A、B,点A、B关于⊙O的反演点分别是A′、B′,点M为⊙C上另一点,关于⊙O的反演点为M′.求证:∠A′M′B′=90°.

(1)如图2,⊙O内有不同的两点A、B,它们的反演点分别是A′、B′,则与∠A′一定相等的角是
(C)
(C)
(A)∠O (B)∠OAB (C)∠OBA (D)∠B′
(2)如图3,⊙O内有一点M,请用尺规作图画出点M的反演点M′;(保留画图痕迹,不必写画法).
(3)如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆O的半径为r,另一个半径为r1的⊙C,作射线OC交⊙C于点A、B,点A、B关于⊙O的反演点分别是A′、B′,点M为⊙C上另一点,关于⊙O的反演点为M′.求证:∠A′M′B′=90°.
分析:(1)先证明△AOB∽△B′OA′,然后根据相似三角形的对应角相等可以推知∠A′=∠OBA;
(2)根据射影定理来找点M′;
(3)根据相似三角形△OMA∽△OA′M′的对应角相等推知∠OMA=∠OB′M′、根据相似三角形△OBM∽△OM′B′的对应角相等推知∠OMB=∠OM′B′,则∠OMA-∠OMB=∠OA′M′-∠OB′M′,∠BMA=∠A′M′B′,即∠A′M′B′=90°.
(2)根据射影定理来找点M′;
(3)根据相似三角形△OMA∽△OA′M′的对应角相等推知∠OMA=∠OB′M′、根据相似三角形△OBM∽△OM′B′的对应角相等推知∠OMB=∠OM′B′,则∠OMA-∠OMB=∠OA′M′-∠OB′M′,∠BMA=∠A′M′B′,即∠A′M′B′=90°.
解答:解:(1)∵⊙O内有不同的两点A、B,它们的反演点分别是A′、B′,
∴
=
;
又∵∠O=∠O,
∴△AOB∽△B′OA′,
∴∠A′=∠OBA;
故答案是:(C);
(2)过M作MN⊥OM交⊙O于点N,连ON.过N作NM'⊥ON交射线OM于点M'.点M'即为所求.如图所示:
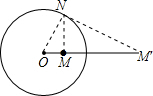
(3)证明:连BM、AM.
∵AB是⊙C直径,
∴∠BMA=90°;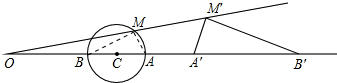
∵∠OA′M′是△A′M′B′的外角,
∴∠OA′M′-∠A′B′M′=∠A′M′B′;
∵点A、M关于⊙O的反演点分别是A′,M′.
∴OA•OA′=r2=OM•OM′,
∵∠O=∠O,
∴△OMA∽△OA′M′,
∴∠OMA=∠OA′M′,
同理:∠OMB=∠OB′M′,
由等式性质知:∠OMA-∠OMB=∠OA′M′-∠OB′M′,
∴∠BMA=∠A′M′B′即∠A′M′B′=90°.
∴
| OA |
| OB′ |
| OB |
| OA′ |
又∵∠O=∠O,
∴△AOB∽△B′OA′,
∴∠A′=∠OBA;
故答案是:(C);
(2)过M作MN⊥OM交⊙O于点N,连ON.过N作NM'⊥ON交射线OM于点M'.点M'即为所求.如图所示:

(3)证明:连BM、AM.
∵AB是⊙C直径,
∴∠BMA=90°;

∵∠OA′M′是△A′M′B′的外角,
∴∠OA′M′-∠A′B′M′=∠A′M′B′;
∵点A、M关于⊙O的反演点分别是A′,M′.
∴OA•OA′=r2=OM•OM′,
∵∠O=∠O,
∴△OMA∽△OA′M′,
∴∠OMA=∠OA′M′,
同理:∠OMB=∠OB′M′,
由等式性质知:∠OMA-∠OMB=∠OA′M′-∠OB′M′,
∴∠BMA=∠A′M′B′即∠A′M′B′=90°.
点评:本题考查了圆的综合题.解题时涉及到的知识点有:相似三角形的判定与性质、圆周角定理、等式的性质等.

练习册系列答案
相关题目
 (2012•浙江一模)如图:直线a∥b,∠1=50°,则∠2=
(2012•浙江一模)如图:直线a∥b,∠1=50°,则∠2=