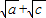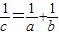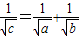题目内容
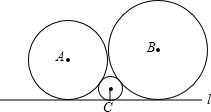
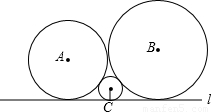
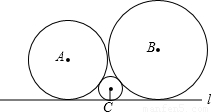
如图,已知圆心为A,B,C的三个圆彼此相切,且均与直线l相切.若⊙A,⊙B,⊙C的半径分别为a,b,c(0<c<a<b),则a,b,c一定满足的关系式为( )

| A、2b=a+c | ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
分析:圆与圆之间的位置关系和有关公切线的知识计算.
解答: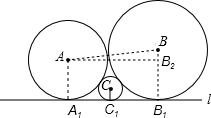 解:过点A、B、C分别向直线l引垂线,垂足分别为A1、B1、C1,易得:
解:过点A、B、C分别向直线l引垂线,垂足分别为A1、B1、C1,易得:
A1B1=
=2
,
同理B1C1=
=2
,
A1C1=
=2
;
又有A1C1+B1C1=A1B1,
可得
=
+
,
两边同除以
可得:
=
+
.
故选D.
 解:过点A、B、C分别向直线l引垂线,垂足分别为A1、B1、C1,易得:
解:过点A、B、C分别向直线l引垂线,垂足分别为A1、B1、C1,易得:A1B1=
| (a+b)2-(b-a)2 |
| ab |
同理B1C1=
| (b+c)2-(b-c)2 |
| bc |
A1C1=
| (a+c)2-(a-c)2 |
| ac |
又有A1C1+B1C1=A1B1,
可得
| ab |
| bc |
| ac |
两边同除以
| abc |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
故选D.
点评:主要考查了圆与圆之间的位置关系和有关公切线的知识.相切两圆的性质:如果两圆相切,那么切点一定在连心线上.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 (2013•太仓市二模)如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4
(2013•太仓市二模)如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4
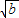 =
=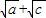
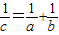
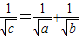
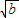 =
=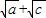
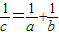
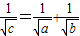
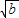 =
=