题目内容
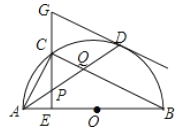
【题目】我们把有一条边是另一条边的2倍的梯形叫做“倍边梯形”,在⊙O中,直径AB=2,PQ是弦,若四边形ABPQ是“倍边梯形”,那么PQ的长为_____.
【答案】1
【解析】
由梯形知AB∥PQ,据此可得AQ=BP,即四边形ABPQ是等腰梯形,再根据“倍边梯形”的定义分AB=2PQ和AB=2AQ两种情况求解可得.
解:如图,
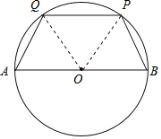
∵四边形ABPQ是梯形,
∴PQ∥AB,
∴AQ=PB,
∵四边形ABPQ是“倍边梯形”,且AB=2,
∴当AB=2PQ时,PQ=1;
当AB=2AQ=2时,AQ=PB=1,
∵OA=OQ=OP=OB=1,
∴△AOQ、△BOP均为等边三角形,
∴∠AOQ=∠BOP=60°,
则∠POQ=60°,
∵OQ=OP=1,
∴△POQ也是等边三角形,
∴PQ=1;
综上,PQ=1,
故答案为:1.

练习册系列答案
相关题目