题目内容
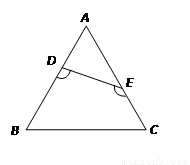
 如图,将等边△ABC竖直向上平移到与BC的距离为2cm的△A′B′C′处,若AB=2
如图,将等边△ABC竖直向上平移到与BC的距离为2cm的△A′B′C′处,若AB=2| 3 |
分析:根据平移的性质得到BC∥B′C′,则∠AEF=∠B=60°,于是可判断△AEF为等边三角形,延长AD交BC于H点,则AH⊥BC,根据等边三角形的性质得AH=
BC=3,由平移的距离为2得到DH=2,则AD=1,然后根据含30度的直角三角形三边的关系可计算出ED=
AD=
,AE=2DE=
.
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
解答: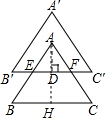 解:∵等边△ABC竖直向上平移到与BC的距离为2cm的△A′B′C′处,
解:∵等边△ABC竖直向上平移到与BC的距离为2cm的△A′B′C′处,
∴BC∥B′C′,
∴∠AEF=∠B=60°,
而∠EAF=60°,
∴△AEF为等边三角形,
延长AD交BC于H点,如图,
∵AD⊥EF,
∴AH⊥BC,
∴AH=
BC=
×2
=3,
∵DH=2,
∴AD=1,
∴ED=
AD=
,
∴AE=2DE=
.
故选C.
 解:∵等边△ABC竖直向上平移到与BC的距离为2cm的△A′B′C′处,
解:∵等边△ABC竖直向上平移到与BC的距离为2cm的△A′B′C′处,∴BC∥B′C′,
∴∠AEF=∠B=60°,
而∠EAF=60°,
∴△AEF为等边三角形,
延长AD交BC于H点,如图,
∵AD⊥EF,
∴AH⊥BC,
∴AH=
| ||
| 2 |
| ||
| 2 |
| 3 |
∵DH=2,
∴AD=1,
∴ED=
| ||
| 3 |
| ||
| 3 |
∴AE=2DE=
2
| ||
| 3 |
故选C.
点评:本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了等边三角形的判定与性质和含30度的直角三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
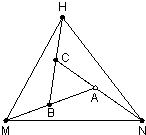 8、如图,将等边△ABC各边向外延伸一倍,构成一个新的△NMH,若△ABC的面积为1,则△NMH的面积是( )
8、如图,将等边△ABC各边向外延伸一倍,构成一个新的△NMH,若△ABC的面积为1,则△NMH的面积是( )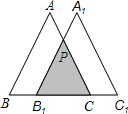 (2012•宁夏)如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3,
(2012•宁夏)如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3,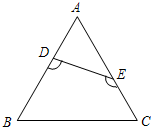 如图,将等边△ABC剪去一个角后,∠BDE+∠CED=
如图,将等边△ABC剪去一个角后,∠BDE+∠CED=