题目内容
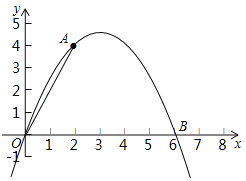
【题目】如图，二次函数
的图象经过点A（2，4）与B（6，0）．
（1）求a，b的值；
（2）点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．
【答案】（1）
，
；（2）16．
【解析】
试题分析：（1）将A（2，4）与B（6，0）代入
，得：
，解得：
；
（2）如图，过A作x轴的垂直，垂足为D（2，0），连接CD，过C作CE⊥AD，CF⊥x轴，垂足分别为E，F，S△OAD=
ODAD=×2×4=4；S△ACD=ADCE=×4×（x﹣2）=2x﹣4；
S△BCD=BDCF=
=
，则S=S△OAD+S△ACD+S△BCD=
=
，∴S关于x的函数表达式为S=（2＜x＜6），∵S==
，∴当x=4时，四边形OACB的面积S有最大值，最大值为16．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
