题目内容
【题目】已知抛物线y=x2﹣2x+1.
(1)求它的对称轴和顶点坐标;
(2)根据图象,确定当x>2时,y的取值范围.
【答案】解:(1)y=x2﹣2x+1=(x﹣1)2 ,
对称轴为直线x=1,顶点坐标为(1,0);
(2)抛物线图象如下图所示: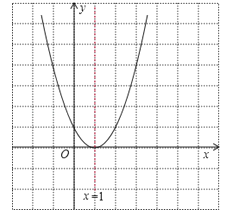
由图象可知当x>2时,y的取值范围是y>1.
【解析】(1)把抛物线解析式化为顶点式即可得出对称轴和顶点坐标;
(2)利用描点法画出图象,根据图象利用数形结合的方法确定当x>2时,y的取值范围即可.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目