Question

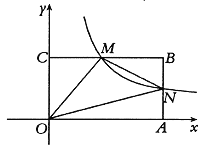
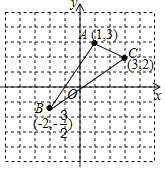
【题目】如图，在平面直角坐标系中有三点（1，3），（3，2），（﹣2，﹣），其中两点同时在反比例函数y＝的图象上，将两点分别记为A，B，另一点记为C．

（1）求反比例函数的解析式；

（2）求直线AB对应的一次函数的解析式；

（3）连接AC、BC，求△ABC的面积．

Answer 1

【答案】（1）y＝；（2）y＝x+；（3）S△ABC＝6．

【解析】

（1）确定A、B、C的坐标即可解决问题；

（2）利用待定系数法即可解决问题；

（3）根据矩形和三角形的面积公式即可得到结论．

（1）∵反比例函数y＝的图象上的点横坐标与纵坐标的积相同，

∴1×3＝（﹣2）×（）＝3≠3×2，

∴点（1，3），（﹣2，），在同一反比例函数的图象上，且k＝3；

∴反比例函数的解析式为y＝；

（2）设直线AB的解析式为y＝mx+n，则，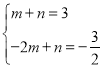

解得，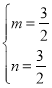

∴直线AB的解析式为y＝x+；

（3）S△ABC＝5×4.5﹣×2×1﹣×3.5×5﹣×3×4.5＝6．