题目内容
如图,线段AB,CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1(升)、y2(升)关于行驶时间x(小时)的函数图象.

(1)分别求y1、y2关于x的函数解析式,并写出定义域;
(2)如果两车同时从相距300千米的甲、乙两地出发,相向而行,匀速行驶,已知轿车的行驶速度比客车的行驶速度快30千米/小时,且当两车在途中相遇时,它们油箱中所剩余的油量恰好相等,求两车的行驶速度.

(1)分别求y1、y2关于x的函数解析式,并写出定义域;
(2)如果两车同时从相距300千米的甲、乙两地出发,相向而行,匀速行驶,已知轿车的行驶速度比客车的行驶速度快30千米/小时,且当两车在途中相遇时,它们油箱中所剩余的油量恰好相等,求两车的行驶速度.
(1) y1=-15x+60,定义域为0≤x≤4. y2=-30x+90,定义域为0≤x≤3;(2)客车60千米/小时,轿车90千米/小时.
试题分析:(1)根据题意设出函数关系式y=kx+b,再根据图象所经过的点利用待定系数法代入可以直接求出函数关系式;
(2)设客车的速度为xkm/时,则小轿车的速度为(x+30)km/时,先根据相遇问题表示出相遇时间,再由图象可以求出客车和小轿车每小时的耗油量,再根据剩余的油相等建立方程求出其解就可以了.
试题解析:(1)设y1=k1x+60,y2=k2x+90.
由题意,得4k1+60=0,
3k2+90=0.
解得 k1=-15,k2=-30.
所以y1=-15x+60,定义域为0≤x≤4.
y2=-30x+90,定义域为0≤x≤3.
(2)设客车的速度为xkm/时,则小轿车的速度为(x+30)km/时,
所以两车的相遇时间为:
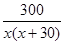 ,
,轿车每小时的耗油量为60÷4=15升,客车每小时耗油量为90÷3=30升.
∵相遇时,它们油箱中所剩余的油量恰好相等,
∴90-30×
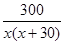 =60-15×
=60-15×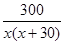 ,
,解得:x=60,
经检验,x=60是原方程的解,
轿车的速度为:60+30=90千米/时.
答:客车60千米/小时,轿车90千米/小时.
考点: 一次函数的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
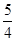 倍,购进数量比第一次少了30支.求第一次每支铅笔的进价是多少元?
倍,购进数量比第一次少了30支.求第一次每支铅笔的进价是多少元?
 =1有增根,则a=________.
=1有增根,则a=________. 的解为()
的解为() ,那么
,那么 的值为( ).
的值为( ).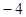


 的解集是 .
的解集是 . 的解是
的解是