题目内容
【题目】已知:△ABC是等边三角形.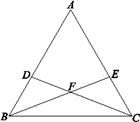
(1)如图,点D在AB边上,点E在AC边上,BD=CE,BE与CD交于点F. 试判断BF与CF的数量关系,并加以证明;
(2)点D是AB边上的一个动点,点E是AC边上的一个动点,且BD=CE,BE与CD交于点F.若△BFD是等腰三角形,求∠FBD的度数.
【答案】
(1)解:BF=CF;理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
在△BCD和△CBE中, 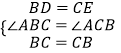 ,
,
∴△BCD≌△CBE(SAS),
∴∠BCD=∠CBE,
∴BF=CF.
(2)解:由(1)得:∠BCD=∠CBE,∠ACB=60°,
设∠BCD=∠CBE=x,
∴∠DBF=60°﹣x,
若△BFD是等腰三角形,分三种情况:
①若FD=FB,则∠FBD=∠FDB>∠A,
∴∠FBD=∠FDB>60°,
但∠FBD>∠ABC,
∴∠FBD<60°,
∴FD=FB的情况不存在;
②若DB=DF,则∠FBD=∠BFD=2x,
∴60°﹣x=2x,
解得:x=20°,
∴∠FBD=40°;
③若BD=BF,如图所示: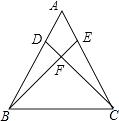
则∠BDF=∠BFD=2x,
在△BDF中,∠DBF+∠BDF+∠BFD=180°,
∴60°﹣x+2x+2x=180°,
解得:x=40°,
∴∠FBD=20°;
综上所述:∠FBD的度数是40°或20°.
【解析】(1)根据题意再由SAS证明△BCD≌△CBE,再由全等三角形的性质可证得结论;
(2)△BFD是等腰三角形,分三种情况:①若FD=FB;②若DB=DF;③若BD=BF,根据三角形的内角和可求出答案.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目