题目内容
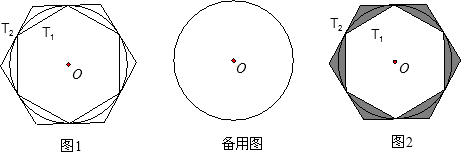
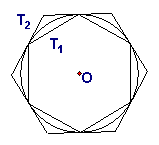
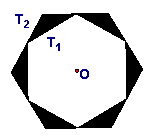
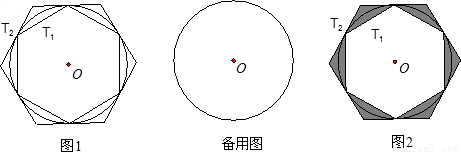
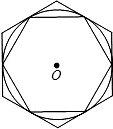如图，⊙O的外切正六边形与内接正六边形的边长之比是________．
2
：3
分析：根据“正六边形的边长=正六边形的半径”将，⊙O的外切正六边形与内接正六边形的边长之比可转化为半径之比来解答．
解答：
解：因为正六边形的边长=正六边形的半径，
所以，⊙O的外切正六边形与内接正六边形的边长之比可转化为：OC：OB．
因为△OBC为直角三角形，
△AOB为等边三角形，
所以∠BOC为30°，
所以OB：OC=cos30°=
．
则OC：OB=2：=2：3
点评：此题不仅考查了正六边形的性质，还考查了转化思想在解题时的应用，是一道基础题．
：3分析：根据“正六边形的边长=正六边形的半径”将，⊙O的外切正六边形与内接正六边形的边长之比可转化为半径之比来解答．
解答：
解：因为正六边形的边长=正六边形的半径，所以，⊙O的外切正六边形与内接正六边形的边长之比可转化为：OC：OB．
因为△OBC为直角三角形，
△AOB为等边三角形，
所以∠BOC为30°，
所以OB：OC=cos30°=
．则OC：OB=2：
=2：3点评：此题不仅考查了正六边形的性质，还考查了转化思想在解题时的应用，是一道基础题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
