题目内容
如图，点D、E是等腰Rt△ABC的斜边BC上两个点（不含端点B、C），且∠DAE=45°，则图中与△EAD相似的三角形为______．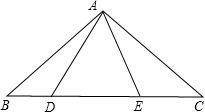
和△EAD相似的三角形有△EBA或△ACD，
理由是：∵△ABC是等腰直角三角形，∠BAC=90°，
∴∠B=∠C=45°，
∵∠EAD=45°，
∴∠B=∠C=∠EAD=45°，
∵∠AEB=∠AED，∠EAD=∠B，
∴△EAD∽△EBA；
同理△EAD∽△ACD．
故答案为：△EBA或△ACD．
理由是：∵△ABC是等腰直角三角形，∠BAC=90°，
∴∠B=∠C=45°，
∵∠EAD=45°，
∴∠B=∠C=∠EAD=45°，
∵∠AEB=∠AED，∠EAD=∠B，
∴△EAD∽△EBA；
同理△EAD∽△ACD．
故答案为：△EBA或△ACD．
练习册系列答案
发散思维新课堂系列答案
相关题目
如图，点D、E是等腰Rt△ABC的斜边BC上两个点（不含端点B、C），且∠DAE=45°，则图中与△EAD相似的三角形为
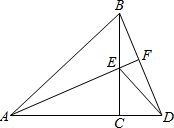已知：如图，△ABC与△CED都是等腰直角三角形，A、C、D三点在同一条直线上，连接BD、AE并延长BE交BD于F点，请说明BD与AE的关系并写出证明过程．
如图，点D、E是等腰Rt△ABC的斜边BC上两个点（不含端点B、C），且∠DAE=45°，则图中与△EAD相似的三角形为________．