题目内容
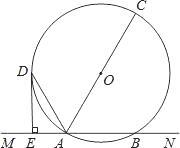
【题目】如图,在![]() 中,
中, ![]() 平分
平分![]() ,
, ![]() 于点
于点![]() .
.
(1)求![]() 的度数.
的度数.
(2)求证: ![]() .
.

【答案】(1)22.5;(2)证明见解析.
【解析】试题分析:(1)因为∠E=∠A,∠CDE=∠BDA,可得∠ECD=∠ABD,由条件知∠ABC=45°且BD平分∠ABC,从而得解.
(2)延长BA,CE交于点F,证△ABD≌△ACF,通过角之间的关系,得到BF=BC,又由CE⊥BD,进而可求解.
试题解析:(1)∵![]()
∴∠ABC=45°
∵BD平分∠ABC
∴∠ABD=![]() ∠ABC=22.5°
∠ABC=22.5°
在△ABD和△ECD中,∠E=∠A,∠CDE=∠BDA
∴∠ECD=∠ABD=22.5°;
(2)证明:如图所示,延长BA,CE交于点F,
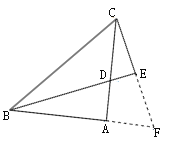
∵∠ABD+∠ADB=90°,∠CDE+∠ACF=90°,
∴∠ABD=∠ACF,
又∵AB=AC,
在Rt△ABD和Rt△ACF中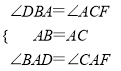
∴Rt△ABD≌Rt△ACF,
∴BD=CF,
在Rt△FBE和Rt△CBE中
∵BD平分∠ABC,
∴∠BCF=∠F,
∵∠BEC=90°
∴∠BEF=∠BEC=90°
∵BE=BE
∴Rt△FBE≌Rt△CBE
∴EF=EC,
∴CF=2CE,
即BD=2CE.

练习册系列答案
相关题目