题目内容
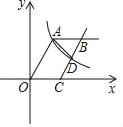
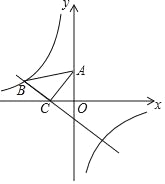
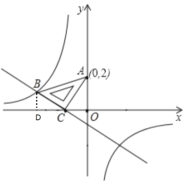
【题目】如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(﹣1,0),点A的坐标为(0,2).一次函数y=kx+b的图象经过点B,C,反比例函数y=![]() 的图象也经过点B.
的图象也经过点B.
(1)求反比例函数的关系式;
(2)直接写出当x<0时,kx+b﹣![]() <0的解集.
<0的解集.
【答案】⑴y=![]() ;
;
⑵![]() .
.
【解析】
(1)作辅助线,证明△BCD≌△AOC,根据已知求出点B的坐标(-3,1),点C的坐标(-1,0),即可求出反比例函数的解析式,
(2)根据反比例函数和一次函数图像的性质,找到直线在双曲线下方的图像即可解题.
解:⑴过B做BD垂直于x轴于D,如下图,
∵点C坐标为(-1,0),点A的坐标为(0,2),
∴tan∠ACO=2,则OC=1,
在Rt△AOC中AO=OC![]() tan∠ACO=2,AC=
tan∠ACO=2,AC=![]() ,(勾股定理),
,(勾股定理),
∴sin∠CAO=![]() ,
,
在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,则BC=AC=![]() 易知△BCD≌△AOC ,则∠BCD=∠CAO,
易知△BCD≌△AOC ,则∠BCD=∠CAO,
∴sin∠BCD=sin∠CAO![]() ,
,
在Rt△BCD中BD=1,CD=2,
∴B的坐标(-3,1),代入y=![]() ,解得:m =-3,
,解得:m =-3,
∴反比例函数的关系式y=![]() ;
;
C坐标为(-1,0),待定系数法解得一次函数的关系式y=![]() ,
,
⑵不等式kx+b-![]() <0的解集即是不等式kx+b<
<0的解集即是不等式kx+b<![]() 的解集,不等式kx+b<
的解集,不等式kx+b<![]() 可把它看成是一次函数的关系式与反比例函数的关系式y=
可把它看成是一次函数的关系式与反比例函数的关系式y=![]() ,则kx+b<
,则kx+b<![]() 的意思是在图象上去找一次函数在反比例函数下方的x的范围即
的意思是在图象上去找一次函数在反比例函数下方的x的范围即![]() .
.

练习册系列答案
相关题目