题目内容
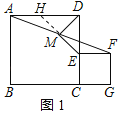
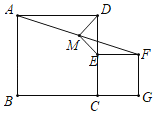
【题目】如图，已知正方形ABCD与正方形CEFG，点E在CD上，点G在BC的延长线上，M是AF的中点，连接DM，EM．
（1）填空：DM与EM数量关系和位置关系为 （直接填写）；
（2）若AB＝4，设CE＝x（0＜x＜4），△MEF面积为y，求y关于x的函数关系式[可利用（1）的结论]，并求出y的最大值；
（3）如果将正方形CEFG绕点C顺时针旋转任意角度，我们发现DM与EM数量关系与位置关系仍未发生改变．
①若正方形ABCD边长AB＝13，正方形CEFG边长CE＝5，当D，E，F三点旋转至同一条直线上时，求出MF的长；
②证明结论：正方形CEFG绕点C顺时针旋转任意角度，DM与EM数量关系与位置关系仍未发生改变．
【答案】（1）DM＝ME，DM⊥EM；（2）y＝
（x﹣2）2+1，最大值1；（3）①
或 
，②见解析
【解析】
（1）证明△MHA≌△MEF得出MH＝ME，AH＝EF＝EC，得出DH＝DE，由等腰直角三角形的性质即可得出结论；
（2）由全等三角形的性质和三角形面积公式得出y关于x的函数关系式，再由二次函数的性质即可得出结果；
（3）①分两种情况，由全等三角形的性质和勾股定理解答即可；
②证明△ADH≌△CDE得出DH＝DE，∠ADH＝∠CDE，得出∠HDE＝90°，即可得出结论．
（1）解：结论：DM＝ME，DM⊥EM．
理由：如图1中，延长EM交AD于H．
∵四边形ABCD是正方形，四边形EFGC是正方形，
∴∠ADE＝∠DEF＝90°，AD＝CD，
∴AD∥EF，
∴∠MAH＝∠MFE，
在△MHA和△MEF中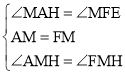
，
∴△MHA≌△MEF（ASA），
∴MH＝ME，AH＝EF＝EC，
∴DH＝DE，
∵∠EDH＝90°，
∴DM＝ME，DM⊥EM；
故答案为：DM＝ME，DM⊥EM；
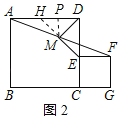
（2）解：作MP⊥DH于P，如图2所示：
∵∠EDH＝90°，DM⊥EM，DM＝ME，
∴MP＝
DH＝（4﹣x），
由（1）得：△MHA≌△MEF，
∴△MHA的面积＝△MEF的面积，
∴y＝AH×MP＝x×（4﹣x）＝（x2﹣4x）＝（x﹣2）2+1，
即y关于x的函数关系式为y＝x2﹣x，
∵y＝x2﹣x＝（x﹣2）2+1，
∴当x＝2时，y有最大值为1；
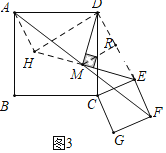
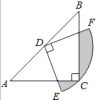
（3）①解：当D、E、F三点在正方形ABCD外同一条直线上时，如图3所示：
连接DE，延长EM到H，使得MH＝ME，连接AH，作MR⊥DE于R，
在△AMH和△FME中，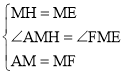
，
△AMH≌△FME（SAS），
∴AH＝EF＝EC，∠MAH＝∠MFE，
∴AH∥DF，
∴∠DAH+∠ADE＝180°，
∴∠DAH+∠CDE＝90°，
∵∠DCE+∠EDC＝90°
∴∠DAH＝∠DCE，
在△DAH和△DCE中，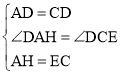
，
∴△DAH≌△DCE（SAS），
∴DH＝DE，∠ADH＝∠CDE，
∴∠HDE＝∠ADC＝90°，
∵ME＝MH，
∴DM⊥EH，DM＝MH＝EM，
∵正方形ABCD边长AB＝CD＝13，正方形CEFG边长CE＝5，
∴在Rt△CDE中，DE＝
＝
＝12，
∵DM＝ME，DM⊥ME，
∴MR⊥DE，MR＝DE＝6，DR＝RE＝6，
∴FR＝RE+EF＝11，
在Rt△FMR中，FM＝
＝
＝；
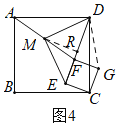
当D、E、F三点在正方形ABCD内同一条直线上时，如图4中，作MR⊥DE于R，
在Rt△MRF中，FM＝＝
＝，
综上所述，满足条件的MF的值为 或 ．
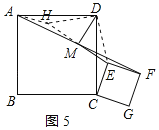
②证明：作AH∥EF交EM的延长线于H，连接DH、DE，如图5所示：
同（1）得：△MHA≌△MEF，
∴MH＝ME，AH＝EF＝CE，
∵AH∥EF，EF⊥CE，
∴AH⊥CE，又∵AD⊥CD，
∴∠DAH＝∠DCE，
在△ADH和△CDE中，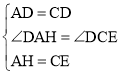
，
∴△ADH≌△CDE（SAS），
∴DH＝DE，∠ADH＝∠CDE，
∴∠HDE＝90°，
∵MH＝ME，
∴DM＝ME，DM⊥EM．
