题目内容
同圆的内接正n边形与外切正n边形边长之比是分析:先根据题意画出图形,再设圆的半径为R,由垂径定理及锐角三角函数的定义即可求解.
解答: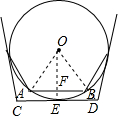 解:如图所示,设圆的半径为R,
解:如图所示,设圆的半径为R,
∵∠AOF=
=
,
∴AB=2AF=2Rsin
;
同理,∵∠BOF=
=
,
∴CD=2DE=2Rtg
,
∴同圆的内接正n边形与外切正n边形边长之比是cos
.
故答案为:cos
.
 解:如图所示,设圆的半径为R,
解:如图所示,设圆的半径为R,∵∠AOF=
| 360° |
| 2n |
| 180° |
| n |
∴AB=2AF=2Rsin
| 180° |
| n |
同理,∵∠BOF=
| 360° |
| 2n |
| 180° |
| n |
∴CD=2DE=2Rtg
| 180° |
| n |
∴同圆的内接正n边形与外切正n边形边长之比是cos
| 180° |
| n |
故答案为:cos
| 180° |
| n |
点评:本题考查的是正多边形和圆、垂径定理及勾股定理,根据题意画出图形,利用数形结合是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目