题目内容
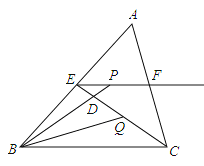
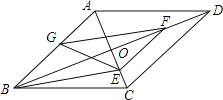
【题目】平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF;②△EFG≌△GBE;③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是______.
【答案】①②④
【解析】
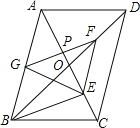
试题解析:令GF和AC的交点为点P,如图
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=![]() CD,
CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴∠FEG=∠BGE(两直线平行,内错角相等),
∵点G为AB的中点,
∴BG=![]() AB=
AB=![]() CD=FE,
CD=FE,
在△EFG和△GBE中,
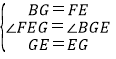 ,
,
∴△EFG≌△GBE(SAS),即②成立,
∴∠EGF=∠GEB,
∴GF∥BE(内错角相等,两直线平行),
∵BD=2BC,点O为平行四边形对角线交点,
∴BO=![]() BD=BC,
BD=BC,
∵E为OC中点,
∴BE⊥OC,
∴GP⊥AC,
∴∠APG=∠EPG=90°
∵GP∥BE,G为AB中点,
∴P为AE中点,即AP=PE,且GP=![]() BE,
BE,
在△APG和△EGP中,
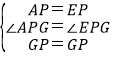 ,
,
∴△APG≌△EPG(SAS),
∴AG=EG=![]() AB,
AB,
∴EG=EF,即①成立,
∵EF∥BG,GF∥BE,
∴四边形BGFE为平行四边形,
∴GF=BE,
∵GP=![]() BE=
BE=![]() GF,
GF,
∴GP=FP,
∵GF⊥AC,
∴∠GPE=∠FPE=90°
在△GPE和△FPE中,
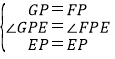 ,
,
∴△GPE≌△FPE(SAS),
∴∠GEP=∠FEP,
∴EA平分∠GEF,即④成立.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目