题目内容
已知:如图,直线y=-
x+4
与x轴相交于点A,与直线y=
x相交于点P.
(1)求点P的坐标;
(2)请判断△OPA的形状并说明理由;
(3)动点E从原点O出发,以每秒1个单位的速度沿着O、P、A的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B,设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:①S与t之间的函数关系式.②当t为何值时,S最大,并求出S的最大值.

| 3 |
| 3 |
| 3 |
(1)求点P的坐标;
(2)请判断△OPA的形状并说明理由;
(3)动点E从原点O出发,以每秒1个单位的速度沿着O、P、A的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B,设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:①S与t之间的函数关系式.②当t为何值时,S最大,并求出S的最大值.

(1)由题意可得:
,
解得
,
所以点P的坐标为(2,2
);
(2)将y=0代入y=-
x+4
,-
x+4
=0,
∴x=4,即OA=4,
作PD⊥OA于D,则OD=2,PD=2
,
∵tan∠POA=
=
,
∴∠POA=60°,
∵OP=
=4,
∴△POA是等边三角形;
(3)①当0<t≤4时,如图,在Rt△EOF中,
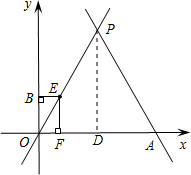 ∵∠EOF=60°,OE=t,
∵∠EOF=60°,OE=t,
∴EF=
t,OF=
t,
∴S=
•OF•EF=
t2.
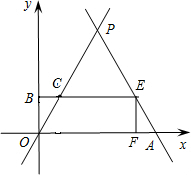
当4<t<8时,如图,设EB与OP相交于点C,
∵CE=PE=t-4,AE=8-t,
∴AF=4-
t,EF=
(8-t),
∴OF=OA-AF=4-(4-
t)=
t,
∴S=
(CE+OF)•EF=
(t-4+
t)×
(8-t),
=-
t2+4
t-8
;
②当0<t≤4时,S=
t2,t=4时,S最大=2
;
当4<t<8时,S=-
t2+4
t-8
=-
(t-
)2+
,
t=
时,S最大=
.
∵
>2
,
∴当t=
时,S最大,最大值为
.
|
解得
|
所以点P的坐标为(2,2
| 3 |
(2)将y=0代入y=-
| 3 |
| 3 |
| 3 |
| 3 |
∴x=4,即OA=4,
作PD⊥OA于D,则OD=2,PD=2
| 3 |
∵tan∠POA=
2
| ||
| 2 |
| 3 |
∴∠POA=60°,
∵OP=
22+(2
|
∴△POA是等边三角形;
(3)①当0<t≤4时,如图,在Rt△EOF中,
 ∵∠EOF=60°,OE=t,
∵∠EOF=60°,OE=t,∴EF=
| ||
| 2 |
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| ||
| 8 |
当4<t<8时,如图,设EB与OP相交于点C,
∵CE=PE=t-4,AE=8-t,
∴AF=4-
| 1 |
| 2 |
| ||
| 2 |
∴OF=OA-AF=4-(4-
| 1 |
| 2 |
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=-
| 3 |
| 8 |
| 3 |
| 3 |
| 3 |
②当0<t≤4时,S=
| ||
| 8 |
| 3 |

当4<t<8时,S=-
| 3 |
| 8 |
| 3 |
| 3 |
| 3 |
| 3 |
| 8 |
| 3 |
| 16 |
| 3 |
| 8 |
| 3 |
| 3 |
t=
| 16 |
| 3 |
| 8 |
| 3 |
| 3 |
∵
| 8 |
| 3 |
| 3 |
| 3 |
∴当t=
| 16 |
| 3 |
| 8 |
| 3 |
| 3 |

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目

 .5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?
.5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?

 交行李托运费.行李费托运费y(元)与行李重量x(千克)之间的函数关系如图所示.
交行李托运费.行李费托运费y(元)与行李重量x(千克)之间的函数关系如图所示.
