题目内容
设a，b，c分别是一元二次方程的二次项系数、一次项系数、常数项，根据下列条件，写出该一元二次方程．
（1）a：b：c=3：4：5，且a+b+c=36；
（2）（a-2）2+|b-4|+
=0．
（1）a：b：c=3：4：5，且a+b+c=36；
（2）（a-2）2+|b-4|+
| c-6 |
分析：（1）设一份为k，表示出a，b及c，代入a+b+c=36列出关于k的方程，求出方程的解得到k的值，确定出a，b及c的值，写出方程即可；
（2）利用非负数之和为0，非负数分别为0求出a，b及c的值，写出方程即可．
（2）利用非负数之和为0，非负数分别为0求出a，b及c的值，写出方程即可．
解答：解：（1）设一份为k，则a=3k，b=4k，c=5k，
∴3k+4k+5k=12k=36，
解得：k=3，
∴a=9，b=12，c=15，
则方程为9x2+12x+15=0；
（2）∵（a-2）2+|b-4|+
=0，
∴a-2=0，b-4=0，c-6=0，
解得：a=2，b=4，c=6，
则方程为2x2+4x+6=0．
∴3k+4k+5k=12k=36，
解得：k=3，
∴a=9，b=12，c=15，
则方程为9x2+12x+15=0；
（2）∵（a-2）2+|b-4|+
| c-6 |
∴a-2=0，b-4=0，c-6=0，
解得：a=2，b=4，c=6，
则方程为2x2+4x+6=0．
点评：此题考查了一元二次方程的一般形式，求出a，b及c的值是解本题的关键．
练习册系列答案
相关题目
的图象都经过点（x1，kx2），求一次函数与反比例函数的解析式．
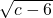=0．