Question

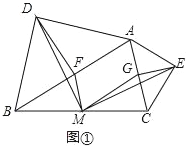
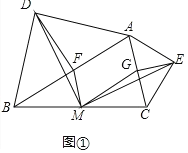
【题目】（发现问题）如图①，在△ABC中，分别以AB、AC为斜边，向△ABC的形外作等腰直角三角形，直角的顶点分别为D、E，点F、M、G分别为AB、BC、AC边的中点，求证：△DFM≌△MGE．

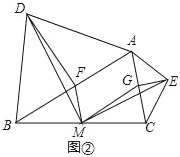
（拓展探究）如图②，在△ABC中，分别以AB、AC为底边，向△ABC的形外作等腰三角形，顶角的顶点分别为D、E，且∠BAD+∠CAE=90°．点F、M、G分别为AB、BC、AC边的中点，若AD=5，AB=6，△DFM的面积为a，直接写出△MGE的面积．

Answer 1

【答案】【发现问题】见解析；【拓展探究】a．

【解析】分析：【发现问题】根据等腰直角三角形的性质得到，DF=FA；，AG=GE，根据三角形的中位线的性质得到FM∥AC,MG∥AB，推出四边形AFMG是平行四边形，根据平行四边形的性质得到FM=AG，MG=FA，∠BFM=∠BAC，∠BAC=∠MGC，即可得到结论；
【拓展探究】根据三角形的中位线的性质得到FM∥AC,MG∥AB,∠MGC=∠BAC=∠BFM，等量代换得到∠DFM=∠MGE，根据余角的性质得到∠1=∠3，根据三角函数的定义 推出 得到△DFM∽△MGE，根据相似三角形的性质即可得到结论．

详解：【发现问题】证明：∵△ADB是等腰直角三角形，F为斜边AB的中点，

∴，DF=FA；

∵△ACE是等腰直角三角形,G为斜边AC的中点,

∴，AG=GE，

∵点F.M、G分别为AB、BC、AC边的中点，

∴FM∥AC,MG∥AB，

∴四边形AFMG是平行四边形，

∴FM=AG，MG=FA，∠BFM=∠BAC，∠BAC=∠MGC，

∴DF=MG，∠DFM=∠MGE，FM=GE，

在△DFM与△MGE中，

∴△DFM≌△MGE.

【拓展探究】∵点F.M、G分别为AB、BC、AC边的中点，

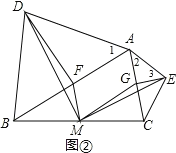
∴FM∥AC,MG∥AB,

∠MGC=∠BAC=∠BFM，

∴∠DFM=∠MGE，

∵

∴∠1=∠3，

∴tan∠1=tan∠3，

即

∴

∵∠DFM=∠MGE，

∴△DFM∽△MGE，

∴

在Rt△ADF中,

∴

∵△DFM的面积为a，

∴