题目内容
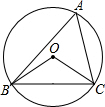（2012•衡水一模）如图，圆O是△ABC的外接圆，连接OB、OC，圆O的半径R=10，sinA=| 3 | 5 |
12
12
．分析：根据圆周角定理求出∠BOC=2∠A，求出∠BOE=∠A，在Rt△BOE中求出BE，根据垂径定理求出BC即可．
解答：解：∵弧BC对的圆周角是∠A，对的圆心角是∠BOC，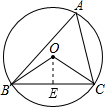
∴∠BOC=2∠A，
过O作OE⊥BC于E，
∵OB=OC，
∴∠BOE=∠COE=
∠BOC，
∴∠BOE=∠A，
∵sinA=
，
∴sin∠BOE=
=
，
∵OB=10，
∴BE=2，
∵OE⊥BC，OE过圆心O，
∴BC=2BE=12，
故答案为：12．
∴∠BOC=2∠A，
过O作OE⊥BC于E，
∵OB=OC，
∴∠BOE=∠COE=
| 1 |
| 2 |
∴∠BOE=∠A，
∵sinA=
| 3 |
| 5 |
∴sin∠BOE=
| 3 |
| 5 |
| BE |
| OB |
∵OB=10，
∴BE=2，
∵OE⊥BC，OE过圆心O，
∴BC=2BE=12，
故答案为：12．
点评：本题考查了垂径定理，圆周角定理，等腰三角形的性质等知识点，关键是构造直角三角形，题目比较好，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
（2012•衡水一模）骰子是一种特别的数字立方体（见右图），它符合规则：相对两面的点数之和总是7，下面四幅图中可以折成符合规则的骰子的是（ ）
（2012•衡水一模）如图，已知二次函数