题目内容
如图,AD是等腰三角形ABC的角平分线,E是AD上一点,连结EB,EC.
(1)求证:△EBD≌△ECD;
(2)若∠BAC=60°,AD=6cm,求BC的长.
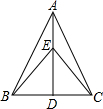
(1)求证:△EBD≌△ECD;
(2)若∠BAC=60°,AD=6cm,求BC的长.

(1)证明:∵AD是等腰三角形ABC的角平分线,
∴∠ADB=∠ADC=90°,BD=CD,
在△EBD与△ECD中,
∴△EBD≌△ECD(SAS);
(2)∵∠BAC=60°,三角形ABC是等腰三角形,
∴三角形ABC是等边三角形,
∴AB=BC=2BD,
在Rt△ADB中,
AB2-BD2=AD2,即BC2-(
BC)2=AD2,
则BC2-(
BC)2=62,
解得BC=4
cm.
∴∠ADB=∠ADC=90°,BD=CD,
在△EBD与△ECD中,
|
∴△EBD≌△ECD(SAS);
(2)∵∠BAC=60°,三角形ABC是等腰三角形,
∴三角形ABC是等边三角形,
∴AB=BC=2BD,
在Rt△ADB中,
AB2-BD2=AD2,即BC2-(
| 1 |
| 2 |
则BC2-(
| 1 |
| 2 |
解得BC=4
| 3 |

练习册系列答案
相关题目