题目内容
【题目】某同学在研究二次函数及其图像性质的问题时,发现了两个重要结论:
①抛物线 y = ax 2 2x + 3(a ≠0) ,不论 a 为何值时,它的顶点都在某条直线上;
②抛物线 y = ax 2 2x + 3(a ≠0),其顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() 得到A点,若把顶点的横坐标增加
得到A点,若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
(1)请你帮忙求出抛物线 y = ax 2 2x + 3的顶点所在直线的解析式,并证明结论②是正确的;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗,并说明理由;
(3)你能把结论①或②(选择其中之一)推广到一般情况吗,请用数学语言表述你的成 果,并给予严格的证明.
【答案】(1)![]() ,证明见解析;(2)(0,3),理由见解析;(3)①的推广:若b、c是常数,对任意的实数
,证明见解析;(2)(0,3),理由见解析;(3)①的推广:若b、c是常数,对任意的实数![]() ,抛物线
,抛物线![]() 的顶点在直线
的顶点在直线![]() 上;②的推广:抛物线
上;②的推广:抛物线![]()
![]() ,将其顶点的横坐标增加或减少
,将其顶点的横坐标增加或减少![]() ,纵坐标增加
,纵坐标增加![]() ,所得到的两个点一定仍在抛物线上;证明见解析.
,所得到的两个点一定仍在抛物线上;证明见解析.
【解析】
(1)首先将抛物线y=ax2+2x+3转化成顶点式,写出用a表示的顶点坐标,消去a写出y关于x的表达式;
(2)观察(1)中的顶点坐标![]() ,因为
,因为![]() ,即横坐标
,即横坐标![]() ,纵坐标
,纵坐标![]() ,即可求得结果;
,即可求得结果;
(3)首先写出抛物线的一般形式,再转化成顶点式,将顶点的横坐标增加
代入一般式,验证纵坐标也增加.
解:(1)方法一:
当![]() 时,
时,![]() 的顶点坐标为(1,2),
的顶点坐标为(1,2),
当![]() 时,
时,![]() 的顶点坐标为(1,4),
的顶点坐标为(1,4),
设抛物线![]() 的顶点在直线
的顶点在直线![]() 上,
上,
将(1,2),(1,4)代入,得:
![]() ,解得:
,解得:![]() ,
,
所以![]() ,
,
即抛物线![]() 的顶点在直线
的顶点在直线![]() ;
;
方法二:
易知![]() 的顶点是
的顶点是![]() ,
,
即![]() ,
,![]() ,
,
消去a得:![]() ,
,
即抛物线![]() 的顶点在直线
的顶点在直线![]() ;
;
证明:抛物线![]() 的顶点是
的顶点是![]() ,
,
由题意得:A(0,3),B(![]() ,3),
,3),
当x=0时,y=3,则点A在抛物线![]() 上,
上,
当x=![]() 时,
时,![]() ,则点B抛物线
,则点B抛物线![]() 上,
上,
(2)直线![]() 上有一点(0,3)不是该抛物线的顶点,
上有一点(0,3)不是该抛物线的顶点,
抛物线![]() 的顶点是
的顶点是![]() ,
,
当![]() 时,横坐标
时,横坐标![]() ,即(0,3)不是抛物线的顶点;
,即(0,3)不是抛物线的顶点;
(3)①的推广
若b、c是常数,对任意的实数![]() ,抛物线
,抛物线![]() 的顶点在直线
的顶点在直线![]() 上.
上.
当![]() 时,则
时,则![]() 的顶点为
的顶点为![]() ,
,
当![]() 时,则
时,则![]() 的顶点为
的顶点为![]() ,
,
将它们代入![]() 得:
得:
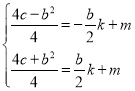 ,
,
解得:![]()
则直线为![]() ,
,
事实上,![]() 时,
时,
![]() ,
,
即抛物线顶点![]() 在直线
在直线![]() 上;
上;
②的推广
猜想:抛物线y = ax 2 2x + 3(a ≠0) ,将其顶点的横坐标增加或减少![]() ,纵坐标增加
,纵坐标增加![]() ,所得到的两个点一定仍在抛物线上.
,所得到的两个点一定仍在抛物线上.
证明:抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
将其横坐标增加或减少![]() ,纵坐标增加
,纵坐标增加![]() ,得到
,得到
![]() ,
,![]()
将![]() 代入
代入![]() 得
得
![]()
=![]()
=![]()
∴点A在抛物线![]() 上,同理可证点B也在抛物线上.
上,同理可证点B也在抛物线上.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案