题目内容
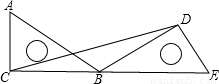
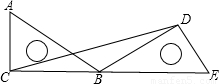
如图，把一块含有30°的直角尺ACB绕点B顺时针旋转，使得点A与CB的延长线上的点E重合，连接CD，则∠BCD的度数是________．
15°
分析：由于把一块含有30°的直角尺ACB绕点B顺时针旋转，使得点A与CB的延长线上的点E重合，那么线段CB旋转后和BD重合，由此可以得到∠DBE=∠ABC=30°，然后利用等腰三角形的性质即可求出∠BCD的度数．
解答：∵把一块含有30°的直角尺ACB绕点B顺时针旋转，使得点A与CB的延长线上的点E重合，
∴线段CB旋转后和BD重合，即BC=BD，∠DBE=∠ABC=30°，
∴∠BCD=∠CDB=15°，
故填空答案：15°．
点评：本题考查旋转的性质，旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．同时也利用了等腰三角形的性质解决问题．
分析：由于把一块含有30°的直角尺ACB绕点B顺时针旋转，使得点A与CB的延长线上的点E重合，那么线段CB旋转后和BD重合，由此可以得到∠DBE=∠ABC=30°，然后利用等腰三角形的性质即可求出∠BCD的度数．
解答：∵把一块含有30°的直角尺ACB绕点B顺时针旋转，使得点A与CB的延长线上的点E重合，
∴线段CB旋转后和BD重合，即BC=BD，∠DBE=∠ABC=30°，
∴∠BCD=∠CDB=15°，
故填空答案：15°．
点评：本题考查旋转的性质，旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．同时也利用了等腰三角形的性质解决问题．
练习册系列答案
相关题目
6、如图，把一块含有30°的直角尺ACB绕点B顺时针旋转，使得点A与CB的延长线上的点E重合，连接CD，则∠BCD的度数是
