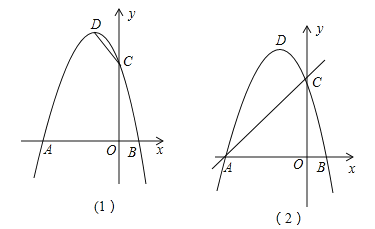题目内容
【题目】二次函数y
x2
x﹣2
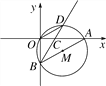
（1）分别求此二次函数图象与x轴的交点A．B和与y轴交点C以及顶点D坐标；
（2）求△ABC的面积；
（3）该二次函数图象上有一点P（x，y），使S△ABP＝S△ABC，请求出P点的坐标．
【答案】（1）A坐标为（﹣1，0）B坐标为（3，0）点C坐标为（0，﹣2）顶点D坐标为（1，
）;（2）4;
（3）（1
，2）、（1
，2）或（2，﹣2）
【解析】
（1）分别令x=0，y=0求点C及A、B坐标，应用顶点坐标公式求对称轴及顶点D坐标；
（2）由（1）求AB、OC可得△ABC的面积；
（3）S△ABP=S△ABC且两个三角形底边重合，则点P到x轴距离为2，分类讨论求出点P坐标即可．
解：（1）当y＝0时，0
x2
x﹣2，解得x1＝3，x2＝﹣1
则点A坐标为（﹣1，0）B坐标为（3，0）
点C坐标为（0，﹣2）
抛物线对称轴为直线x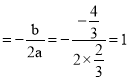
则顶点D坐标为（1，
）
（2）S△ABC
（3）∵S△ABP＝S△ABC
∴点P到AB边的距离为2
当点P在x轴上方时，2x2x﹣2
解得x1＝1
，x2＝1
∴点P坐标为（1，2）或（1，2）
当点P在x轴下方时，点P与点C关于直线x＝1对称
则P点坐标为（2，﹣2）
∴点P坐标为（1，2）、（1，2）或（2，﹣2）
练习册系列答案
相关题目
