题目内容
(本题10分).如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
【小题1】(1)求证:DE平分∠BDC;
【小题2】(2)若点M在DE上,且DC=DM,求证:ME=BD.
【小题1】(1)在等腰直角△ABC中,
∵∠CAD=∠CBD=15o,
∴∠BAD=∠ABD=45o﹣15o=30o,
∴BD=AD,
∴△BDC≌△ADC,
∴∠DCA=∠DCB=45o.
由∠BDM=∠ABD+∠BAD=30o+30o=60o,
∠EDC=∠DAC+∠DCA=15o+45o=60o,
∴∠BDM=∠EDC,
∴DE平分∠BDC;
【小题2】(2)如图,连接MC,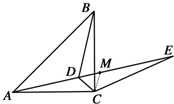
∵DC=DM,且∠MDC=60°,
∴△MDC是等边三角形,即CM=CD.
又∵∠EMC=180°﹣∠DMC=180°﹣60°=120°,
∠ADC=180°﹣∠MDC=180°﹣60°=120°,
∴∠EMC=∠ADC.
又∵CE=CA,
∴∠DAC=∠CEM=15°,
∴△ADC≌△EMC,
∴ME=AD=DB.
解析

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 (AB+AC)。
(AB+AC)。
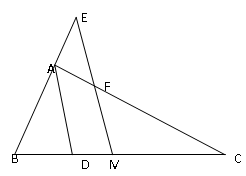
 题满分10分),如图,在△ABC中,AD是∠BAC的平分线,M是BC的中点,过M作ME∥AD交BA延长线于E,交AC于F,求证:BE=CF=
题满分10分),如图,在△ABC中,AD是∠BAC的平分线,M是BC的中点,过M作ME∥AD交BA延长线于E,交AC于F,求证:BE=CF= (AB+AC)。
(AB+AC)。
 (AB+AC)。
(AB+AC)。