题目内容
已知AB为⊙O的直径，弦CD⊥AB，垂足为H.求证：AH•AB=AC2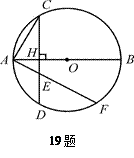
略解析:
(1) 连结CB，∵AB是⊙O的直径，∴∠ACB=90°.
而∠CAH=∠BAC，∴△CAH∽△BAC .
∴
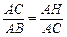， 即AH•AB="AC2" .
(2) 连结FB，易证△AHE∽△AFB
∴ AE•AF=AH•AB
∴ AE•AF=AC
(也可连结CF，证△AEC∽△ACF)
(3) 结论AP•AQ=AC2成立 .
(1) 连结CB，∵AB是⊙O的直径，∴∠ACB=90°.
而∠CAH=∠BAC，∴△CAH∽△BAC .
∴
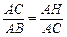， 即AH•AB="AC2" .(2) 连结FB，易证△AHE∽△AFB
∴ AE•AF=AH•AB
∴ AE•AF=AC
(也可连结CF，证△AEC∽△ACF)
(3) 结论AP•AQ=AC2成立 .
练习册系列答案
相关题目
如图，已知AB为⊙O的直径，PA，PC是⊙O的切线，A，C为切点，∠BAC=30°．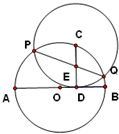
22、如图，已知AB为⊙O的直径，C为⊙O上一点，CD⊥AB于D，AD=9，BD=4，以C为圆心，CD为半径的圆与⊙O相交于P，Q两点，弦PQ交CD于E，则PE•EQ的值是（ ）
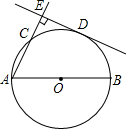如图所示，已知AB为⊙O的直径，C、D是直径AB同侧圆周上两点，且弧CD=弧BD，过D作DE⊥AC于点E，求证：DE是⊙O的切线．
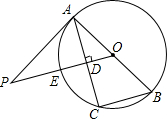（2013•沙市区一模）如图，已知AB为⊙O的直径，PA与⊙O相切与点A，线段OP与弦AC垂直并相交于点D，OP与⊙O相交于点E，连接BC．
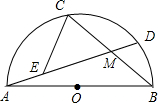已知AB为半圆的直径，弦AD、BC相交于M，点E在AM上，且∠CEM=∠B，AB=1，则cos∠AMC的值等于线段（ ）的长．