Question

【题目】在等边△ABC中，D是AC边上一点，连接BD，将△BCD绕点B逆时针旋转60°得到△BAE，连接ED，若BC=5，BD=4，有下列结论：①AE∥BC；②∠ADE=∠BDC；③△BDE是等边三角形；④△ADE的周长是9.其中正确的个数是（ ）

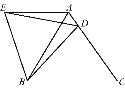
A. 4 B. 3 C. 2 D. 1

Answer 1

【答案】B

【解析】

首先由旋转的性质可知∠EAB=∠ABC=60°，所以可得AE∥BC；由△ABC是等边三角形得出AC=AB=BC=5，根据图形旋转的性质得出AE=CD，BD=BE，故可得出AE+AD=AD+CD=AC=5，由∠EBD=60°，BE=BD即可判断出△BDE是等边三角形，故DE=BD=4，故△AED的周长=AE+AD+DE=AC+BD=9，综上可得答案．

∵△ABC是等边三角形，

∴∠ABC=∠C=60°，

∵将△BCD绕点B逆时针旋转60°，得到△BAE，

∴∠EAB=∠C=∠ABC=60°，

∴AE∥BC，故结论①正确；

∵没有条件证明∠ADE=∠BDC，

∴结论②错误，

∵△ABC是等边三角形，

∴AC=AB=BC=5，

∵△BAE是△BCD逆时针旋转60°得出，

∴AE=CD，BD=BE，∠EBD=60°，

∴AE+AD=AD+CD=AC=5，

∵∠EBD=60°，BE=BD，

∴△BDE是等边三角形，故结论③正确；

∴DE=BD=4，

∴△AED的周长=AE+AD+DE=AC+BD=9，故结论④正确；

综上所述：①③④结论正确，共3个，

故选B.