题目内容
【题目】把正整数
排列成如图所示得一个数表.
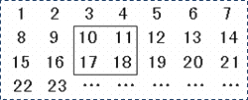
⑴用一个正方形在表中随意框住4个数，把其中最小的数记为
，另外三个数用含
的式子表示出来，从大到小依次是 _____ ，_______ ，________ ；
⑵.当被框住的4个数之和等于416时， 
的值是多少？
⑶被框住的4个数之和能否等于622？如果能，请求出
的值；如果不能，请说明理由.
【答案】 
【解析】试题分析：（1）根据数表的排列规律以及被框住的四个数的相邻和相对之间的数据大小，可用含
的式子表示另外三个数；
（2）根据⑴表示出的四个数据代数式，以“4个数之和等于416”建立一个一元一次方程可以求出
的值；
（3）存在性问题一般要建设“存在”，然后在此基础上探究其存在的可能性.故本题应先假设“被框住的4个数之和等于622”，然后按⑵问的方式解答求是否有符合条件的
，有符合条件的
就“能”，没有符合条件的
，说明就“不能”.
试题解析：（1）若被框住最小的数记为
，另外三个数用含
的式子表示出来，从大到小依次为
， 
， 
；
（2）根据题意和⑴问可列方程为： 
，
解得： 
（3）假设“被框住的4个数之和等于622”，
根据题意和⑴问可以列方程： 
，
解得： 
；
因为数表中的数据均要求均为正整数，所以
不符合条件，换句话说“没有符合条件的
，使被框住的4个数之和等于622”.
练习册系列答案
相关题目
