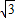题目内容
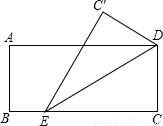
(1)如图所示折叠长方形的一边AD,点D落在BC边的点F处,已知AB=12cm,BC=13cm,求EC的长.(2)已知|2011-x|+
| x-2012 |
分析:(1)根据图形翻折变换的性质可知AD=AF=13,DE=EF,在Rt△ABF中,利用勾股定理可求出BF的长,进而可求出CF的长,设CE的长是x,在Rt△CEF中利用勾股定理即可求出CE的长;
(2)先根据x-2012≥0可去掉绝对值符号,再把等式两边平方即可得出答案.
(2)先根据x-2012≥0可去掉绝对值符号,再把等式两边平方即可得出答案.
解答:解:(1)∵△AFE是△ADE沿AE翻折而成,
∴AD=AF=13,DE=EF,
在Rt△ABF中,设
BF=
=
=5,
∴CF=BC-BF=13-5=8,
设CE=x,则EF=12-x,
在Rt△CEF,EF2=CE2+CF2,即(12-x)2=x2+82,
解得x=
.
故答案为:
cm;
(2)∵
≥0,
∴x≥2012,
∴原式可化为:x-2011+
=x+1,
即
=2012,
两边平方得,x-2012=20122,
移项得,x-20122=2012.
故答案为:2012.
∴AD=AF=13,DE=EF,
在Rt△ABF中,设
BF=
| AF2-AB2 |
| 132-122 |
∴CF=BC-BF=13-5=8,
设CE=x,则EF=12-x,
在Rt△CEF,EF2=CE2+CF2,即(12-x)2=x2+82,
解得x=
| 10 |
| 3 |
故答案为:
| 10 |
| 3 |
(2)∵
| x-2012 |
∴x≥2012,
∴原式可化为:x-2011+
| x-2012 |
即
| x-2012 |
两边平方得,x-2012=20122,
移项得,x-20122=2012.
故答案为:2012.
点评:本题考查的是图形翻折的性质、勾股定理及二次根式有意义的条件,熟知以上知识是解答此题的关键.

练习册系列答案
相关题目
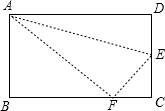
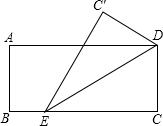 将一张矩形纸片ABCD如图所示折叠,使顶点C落在C′点.已知AB=2,∠DEC′=30°,则折痕DE的长为( )
将一张矩形纸片ABCD如图所示折叠,使顶点C落在C′点.已知AB=2,∠DEC′=30°,则折痕DE的长为( )| A、2 | ||
B、2
| ||
| C、4 | ||
| D、1 |
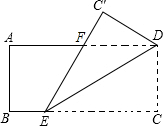 (2007•攀枝花)将一张矩形纸片ABCD按如图所示折叠,使顶点C落在C′点.已知AB=2,∠DEC′=30°,则EF的长是( )
(2007•攀枝花)将一张矩形纸片ABCD按如图所示折叠,使顶点C落在C′点.已知AB=2,∠DEC′=30°,则EF的长是( ) 动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.