题目内容
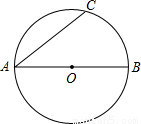
 已知AB、AC为⊙O的两条弦
已知AB、AC为⊙O的两条弦
(1)用直尺(没有刻度)和圆规作出弧BC的中点D;
(2)连接OD,则OD∥AC吗?若成立,请证明;若不成立,请添加一个适当的条件,使之成立,再证明.
解:(1)作法:①连接BC,
②分别以B、C点为圆形,OB为半径画弧,设两弧交于点M,
③连接OM,设OM与圆交于点D,
④则点D为所求作的点.

(2)不成立,添加:AB是直径,
证明:连接BC,OC,
∵点D为 的中点,
的中点,
∴∠COD=∠BOD,
∴∠BOC=2∠BOD,
∵∠BOC=2∠CAB,
∴∠BOD=∠CAB,
∴AC∥OD.

分析:(1)连接BC后,过O点做BC的垂线,则垂线与 的交点即为D点,(2)不成立,添加:AB是直径,连接BC,OC,由点D为
的交点即为D点,(2)不成立,添加:AB是直径,连接BC,OC,由点D为 的中点,推出∠COD=∠BOD,可知∠BOC=2∠BOD,再由∠BOC=2∠CAB,通过等量代换可得∠BOD=∠CAB,即可推出∠AC∥OD.
的中点,推出∠COD=∠BOD,可知∠BOC=2∠BOD,再由∠BOC=2∠CAB,通过等量代换可得∠BOD=∠CAB,即可推出∠AC∥OD.
点评:本题主要考查过线外一点作线段的中垂线,圆周角定理,平行线的判定等知识点,关键在于正确的作出图形,熟练的运用相关的性质定理推出∠BOC=2∠BOD,∠BOC=2∠CAB,继而推出∠BOD=∠CAB.
②分别以B、C点为圆形,OB为半径画弧,设两弧交于点M,
③连接OM,设OM与圆交于点D,
④则点D为所求作的点.

(2)不成立,添加:AB是直径,
证明:连接BC,OC,
∵点D为
 的中点,
的中点,∴∠COD=∠BOD,
∴∠BOC=2∠BOD,
∵∠BOC=2∠CAB,
∴∠BOD=∠CAB,
∴AC∥OD.

分析:(1)连接BC后,过O点做BC的垂线,则垂线与
 的交点即为D点,(2)不成立,添加:AB是直径,连接BC,OC,由点D为
的交点即为D点,(2)不成立,添加:AB是直径,连接BC,OC,由点D为 的中点,推出∠COD=∠BOD,可知∠BOC=2∠BOD,再由∠BOC=2∠CAB,通过等量代换可得∠BOD=∠CAB,即可推出∠AC∥OD.
的中点,推出∠COD=∠BOD,可知∠BOC=2∠BOD,再由∠BOC=2∠CAB,通过等量代换可得∠BOD=∠CAB,即可推出∠AC∥OD.点评:本题主要考查过线外一点作线段的中垂线,圆周角定理,平行线的判定等知识点,关键在于正确的作出图形,熟练的运用相关的性质定理推出∠BOC=2∠BOD,∠BOC=2∠CAB,继而推出∠BOD=∠CAB.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
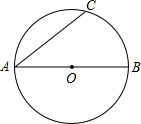 已知AB、AC为⊙O的两条弦
已知AB、AC为⊙O的两条弦