题目内容
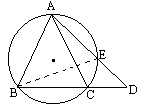
已知:如图,圆内接△ABC中,AB=AC,D是BC边上一点,E是直线AD和△ABC外接圆的交点.(1)证明:AB2=AD·AE;(2)当D为BC延长线上一点时,(1)的结论还成立吗?如果成立,请证明;不成立,请说明理由.

答案:
解析:
解析:
|
(1)连接BE,则∠E=∠C. ∵ AB=AC,∴∠C=∠ABC,∠E=∠ABC.又∠ BAD=∠EAB,故△ABD∽△AEB,(2)当D是BC延长线上一点时,第(1)问的结论仍能成立. 如图,连接 BE,则∠AEB=∠ABC.
又∠ BAE=∠DAB,故△ABD∽△AEB, |

练习册系列答案
相关题目
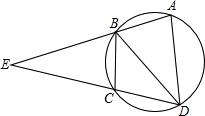 已知:如图,圆内接四边形ABCD的一组对边AB、DC的延长线相交于点E,且∠DBA=∠EBC.求证:AD•BE=EC•BD.
已知:如图,圆内接四边形ABCD的一组对边AB、DC的延长线相交于点E,且∠DBA=∠EBC.求证:AD•BE=EC•BD. 2、已知:如图,圆内接四边形ABCD中,∠BAD=65°,则∠BCD=
2、已知:如图,圆内接四边形ABCD中,∠BAD=65°,则∠BCD= 已知:如图,圆内接四边形ABCD,过C点作对角线BD的平行线交AD的延长线于E点.
已知:如图,圆内接四边形ABCD,过C点作对角线BD的平行线交AD的延长线于E点.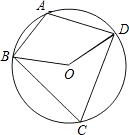 已知,如图,圆内接四边形ABCD中,
已知,如图,圆内接四边形ABCD中,
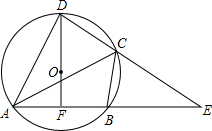 (2009•甘孜州)已知:如图,圆内接四边形ABCD的两边AB,DC的延长线相交于点E,DF经过⊙O的圆心,交AB于点F,AB=BE,连接AC,且OD=3,FA=FB=
(2009•甘孜州)已知:如图,圆内接四边形ABCD的两边AB,DC的延长线相交于点E,DF经过⊙O的圆心,交AB于点F,AB=BE,连接AC,且OD=3,FA=FB=