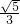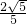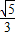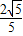题目内容
Rt△ABC在中,∠ACB=90°,CD是Rt△ABC斜边AB上的高,垂足为D.已知AC=3,AD=2,则tanB的值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据题中条件可知∠B=∠DCA,所以把做题方向转化到△ADC中,而在△ADC中,根据勾股定理可求得CD,从而用正切即可解答.
解答: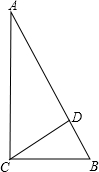 解:∵∠B+∠BCD=90°,∠BCD+∠ACD=90°,
解:∵∠B+∠BCD=90°,∠BCD+∠ACD=90°,
∴∠B=∠ACD.
∴tanB=tanACD=
.
∵AC=3,AD=2,
∴CD=
∴tanB=
=
.
故选B.
 解:∵∠B+∠BCD=90°,∠BCD+∠ACD=90°,
解:∵∠B+∠BCD=90°,∠BCD+∠ACD=90°,∴∠B=∠ACD.
∴tanB=tanACD=
| AD |
| CD |
∵AC=3,AD=2,
∴CD=
| 5 |
∴tanB=
| 2 | ||
|
2
| ||
| 5 |
故选B.
点评:此题主要考查了解直角三角形的能力.关键是找出∠B=∠ACD,会利用三角函数的定义求值.

练习册系列答案
相关题目
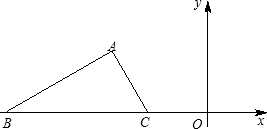
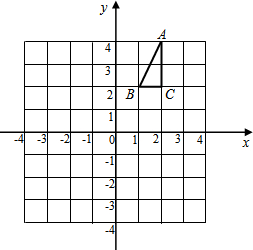 Rt△ABC在如图所示的平面直角坐标系中.
Rt△ABC在如图所示的平面直角坐标系中.