题目内容
【题目】如图,矩形OABC在第一象限,OA,OC分别于x轴,y轴重合,面积为6.矩形与双曲线y=![]() (x>0)交BC于M,交BA于N,连接OB,MN,若2OB=3MN,则k=
(x>0)交BC于M,交BA于N,连接OB,MN,若2OB=3MN,则k= 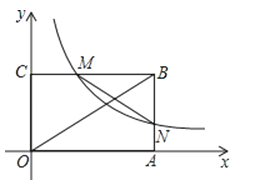
【答案】2
【解析】解:设点A的横坐标为a,则OA=a,
∵矩形OABC的面积为6,
∴OC=![]() ,
,
∴AN=![]() ,
,
∵点M在BC上,
∴![]() =
=![]() ,
,
解得x=![]() ,
,
∴CM=![]() ,
,
∴BM=BC﹣CM=a﹣![]() ,
,
BN=AB﹣AN=![]() ﹣
﹣![]() ,
,
由勾股定理得,OB2=OA2+AB2=a2+(![]() )2=
)2=![]() (a4+36),
(a4+36),
MN2=BM2+BN2=(a﹣![]() )2+(
)2+(![]() ﹣
﹣![]() )2=
)2=![]() (6﹣k)2+
(6﹣k)2+![]() (6﹣k)2=
(6﹣k)2=![]() (6﹣k)2
(6﹣k)2![]() (a4+36),
(a4+36),
∵2OB=3MN,
∴4OB2=9MN2 ,
∴4×![]() (a4+36)=9×
(a4+36)=9×![]() (6﹣k)2
(6﹣k)2![]() (a4+36),
(a4+36),
∴(6﹣k)2=16,
解得k1=2,k2=10,
∵矩形OABC的面积为6,点B在双曲线上方,
∴k<6,
∴k的值为2.
所以答案是:2.
【考点精析】关于本题考查的矩形的判定方法,需要了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能得出正确答案.

【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?