题目内容
【题目】为迎接五一国际劳动节，某校团委组织了“劳动最光荣”有奖征文活动，并设立了一、二、三等奖．学校计划派人根据设奖情况买50件奖品，其中二等奖件数比一等奖件数的2倍还少10件，三等奖所花钱数不超过二等奖所花钱数的1.5倍．各种奖品的单价如下表所示．如果计划一等奖买x件，买50件奖品的总钱数是w元．
（1）求w与x的函数关系式及自变量
的取值范围；
（2）请你计算一下，如何购买这三种奖品所花的总钱数最少？最少是多少元？
一等奖 | 二等奖 | 三等奖 |
12元 | 10元 | 5元 |
【答案】（1）10≤x＜20，且x为整数；（2）一等奖10件，二等奖10件，三等奖30件，花费最少，370元．
【解析】
（1）首先求出w与x的函数关系式，再根据题意列出不等式组即可求解．
（2）因为k=17，故根据反函数的性质可知w随x的增大而增大．根据题1可求最小值．
（1）w=12x+10（2x﹣10）+5[50﹣x﹣（2x﹣10）]=17x+200．
由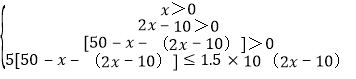
解得：10≤x＜20
故自变量的取值范围是10≤x＜20，且x为整数．
（2）w=17x+200．
∵k=17＞0，∴w随x的增大而增大，当x=10时，有w最小值．
最小值为w=17×10+200=370．
答：一等奖买10件，二等奖买10件，三等奖买30件时，所花的钱数最少，最少钱数是370元．
目标测试系列答案
【题目】供电局的电力维修工甲、乙两人要到30千米远的A地进行电力抢修．甲骑摩托车先行，
小时后乙开抢修车载着所需材料出发，结果甲、乙两人同时到达．已知抢修车的速度是摩托车的1.5倍，求摩托车的速度．
（1）设摩托车的速度为x千米／时，利用速度、时间、路程之间的关系填写下表．
（要求：填上适当的代数式，完成表格）
速度（千米／时） | 所走的路程（千米） | 所用时间（时） | |
摩托车 | x | 30 | |
抢修车 | 30 |
（2）列出方程，并求摩托车的速度．
