��Ŀ����
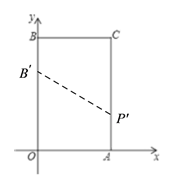
����Ŀ����֪��A��a��0����B��0��b������![]() ���ֱ����A��B��x�ᡢy��Ĵ��߽��ڵ�C����ͼ����P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-B-C-A-O��·���ƶ���
���ֱ����A��B��x�ᡢy��Ĵ��߽��ڵ�C����ͼ����P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-B-C-A-O��·���ƶ���
��1��д��A��B��C��������ꣻ
��2������P�ƶ���6��ʱ�������ʱP���λ�ã���д����P��λ�����ꣻ
��3�����ᣨ2����B��P���㣬���߶�BP����ƽ��h����λ��h��0�����õ�B��P�䣬��B��P�佫�ı���OACB���ܳ��ֳ���ȵ������֣���h��ֵ��

���𰸡���1��A��4��0����B��0��6����C��4��6������2��P��4��4������3��h��ֵΪ2��
�����������������
��1����![]() �ɽ����a=4��b=6���Ӷ��ɵõ�A��B������ֱ�Ϊ��4��0���ͣ�0��6�����������ɵõ�C������Ϊ��4��6����
�ɽ����a=4��b=6���Ӷ��ɵõ�A��B������ֱ�Ϊ��4��0���ͣ�0��6�����������ɵõ�C������Ϊ��4��6����
��2���������֪��6��ʱ����P�˶���12����λ���ȣ��ɵ�A��B��C������ɵ�OA=BC=4��AC=OB=6���ɴ˼��ɵõ���P������Ϊ��4��4����
��3������ͼ����OB��+AP��=![]() (OB+AC)ʱ��BPƽ���ı���OACBA���ܳ����ɴ˸�������ɵã�6-h+6-2-h=6�����h=2.
(OB+AC)ʱ��BPƽ���ı���OACBA���ܳ����ɴ˸�������ɵã�6-h+6-2-h=6�����h=2.
���������
��1����![]() ��
��
��a-4=0��b-6=0�����a=4��b=6��
����A��B������ֱ�Ϊ��4��0���ͣ�0��6����
����C��������4��6����
��2���ߵ�Pÿ���ƶ�6����λ���ȣ�
��6��ʱ����P�ƶ���12����λ���ȣ�
��OA=BC=4��AC=OB=6��
����6��ʱ����P������Ϊ��4��4����
��3������ͼ��ʾ��������ɵõ�OB��+AP��=![]() (OB+AC)ʱ��BPƽ���ı���OACBA���ܳ���
(OB+AC)ʱ��BPƽ���ı���OACBA���ܳ���
��6-h+6-2-h=6�����h=2.
����h=2ʱ��B��P��ƽ���ı���OABC���ܳ�.