题目内容
某地震救援队探测出一建筑物废墟下方点C处有生命迹象，已知废墟两侧地面上两探测点A，B相距10米，探测线与地面的夹角分别是22°和58°（如图），试确定生命所在点C的深度．（结果精确到0.1米，参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）
【答案】分析：根据AB的长度及∠BAC的度数可求出AC的长度，然后根据CD=ACsin∠BAC即可得出答案．
解答：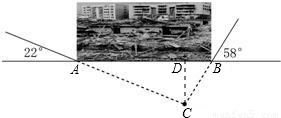
解：过点C作CD垂直AB于D，
由题意得：AB=10，∠BAC=22°，
∴AC=ABcos∠BAC=9.3，
∴CD=ACsin∠BAC=3.4米．
点评：本题考查解直角三角形的应用，属于基础题，对于此类题目关键是熟练掌握正弦、余弦、正切、余切在直角三角形中的表示形式．
解答：
解：过点C作CD垂直AB于D，由题意得：AB=10，∠BAC=22°，
∴AC=ABcos∠BAC=9.3，
∴CD=ACsin∠BAC=3.4米．
点评：本题考查解直角三角形的应用，属于基础题，对于此类题目关键是熟练掌握正弦、余弦、正切、余切在直角三角形中的表示形式．
练习册系列答案
相关题目
25、某地震救援队探测出一建筑物废墟下方点C处有生命迹象，已知废墟两侧地面上两探测点A，B相距10米，探测线与地面的夹角分别是22°和58°（如图），试确定生命所在点C的深度．（结果精确到0.1米，参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）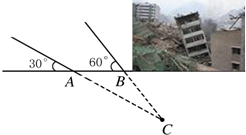
（2011•荔湾区一模）某地震救援队探测出某建筑物废墟下方点C处有生命迹象，已知废墟一侧地面上两探测点A，B相距3米，探测线与地面的夹角分别是30°和60°（如图），试确定生命所在点C的深度．（结果保留根号）
，所以BD＝________＝________．
，所以AD＝________＝________．
≈2.6(米)．
