题目内容
【题目】如图:已知在△ABC中,∠ACB=90°,AC=BC=1,点D是AB上任意一点,AE⊥AB,且AE=BD,DE与AC相交于点F. 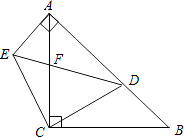
(1)试判断△CDE的形状,并说明理由.
(2)是否存在点D,使AE=AF?如果存在,求出此时AD的长,如果不存在,请说明理由.
【答案】
(1)解:△CDE是等腰直角三角形.理由如下:
∵∠ACB=90°,AC=BC,
∴∠B=∠BAC=45°,
∵AE⊥AB,
∴∠CAE=90°﹣45°=45°,
∴∠B=∠CAE,
在△ACE和△BCD中, 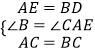 ,
,
∴△ACE≌△BCD(SAS),
∴CD=CE,∠ACE=∠BCD,
∵∠ACD+∠BCD=∠ACB=90°,
∴∠DCE=∠ACD+∠ACE=90°,
∴△CDE是等腰直角三角形
(2)解:存在AD=1.理由如下:
∵AE=AF,∠CAE=45°,
∴∠AEF=∠AFE= ![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠ADE=90°﹣67.5°=22.5°,
∵△CDE是等腰直角三角形,
∴∠CDE=45°,
∴∠ADC=22.5°+45°=67.5°,
在△ACD中,∠ACD=180°﹣45°﹣67.5°=67.5°,
∴∠ACD=∠ADC,
∴AD=AC=1.
【解析】(1)根据等腰直角三角形的性质求出∠B=∠BAC=45°,再求出∠CAE=45°,从而得到∠B=∠CAE,再利用“边角边”证明△ACE和△BCD全等,根据全等三角形对应边相等可得CD=CE,全等三角形对应角相等可得∠ACE=∠BCD,再求出∠DCE=90°,从而得解;(2)根据等腰三角形两底角相等求出∠AEF=∠AFE=67.5°,再根据直角三角形两锐角互余求出∠ADE=22.5°,然后求出∠ADC=67.5°,利用三角形的内角和定理求出∠ACD=67.5°,从而得到∠ACD=∠ADC,根据等角对等边即可得到AD=AC.