Question

【题目】如图，已知四边形OABC是平行四边形，点A（2，2）和点C（6，0），连结CA并延长交y轴于点D．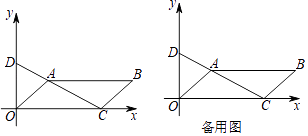

（1）求直线AC的函数解析式．
（2）若点P从点C出发以2个单位/秒沿x轴向左运动，同时点Q从点O出发以1个单位/秒沿x轴向右运动，过点P、Q分别作x轴垂线交直线CD和直线OA分别于点E、F，猜想四边形EPQF的形状（点P、Q重合除外），并证明你的结论．
（3）在（2）的条件下，当点P运动多少秒时，四边形EPQF是正方形？

Answer 1

【答案】
（1）解：设直线AC的解析式为y=kx+b，

∵点A（2，2）和点C（6，0），

∴ ，

∴ ，

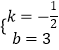∴直线AC的解析式为y=﹣ x+3

（2）解：如图1，

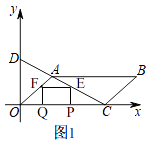
∵点A的坐标为（2，2），

∴直线OA的解析式为y=x，

∵点Q从点O出发以1个单位/秒沿x轴向右运动，

∴OQ=t，

∴F（t，t），

∴FQ=t，

∵点P从点C出发以2个单位/秒沿x轴向左运动，

∴CP=2t，

∴OP=6﹣2t，

由（1）知，直线AC的解析式为y=﹣ x+3，

∴E（6﹣2t，t），

∴PE=t，

∴PE=FQ，

∵FQ⊥x轴，PE⊥x轴，

∴∠PQF=90°，FQ∥PE，

∵PE=FQ，

∴四边形PEFQ是平行四边形，

∵∠PQF=90°，

∴平行四边形PEFQ是矩形

（3）解：由（2）知，PC=2t，OQ=t，PE=t，

∴PQ=OC﹣OQ﹣CP=6﹣t﹣2t=6﹣3t，或PQ=OQ+CP﹣OC=3t﹣6，

∵四边形PEFQ是正方形，

∴PQ=PE，

∴6﹣3t=t或3t﹣6=t，

∴t= 或t=3，即：点P运动 秒或3秒时，四边形EPQF是正方形

【解析】（1）利用待定系数法即可求出直线AC的解析式；（2）先利用待定系数法求出直线OA的解析式，进而求出点E，F坐标，即可得出PE=FQ，即可得出结论；（3）先分两种情况（点Q在点P左侧或右侧）求出PQ，利用PE=PQ建立方程即可求出时间．

【考点精析】关于本题考查的确定一次函数的表达式和正方形的判定方法，需要了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；先判定一个四边形是矩形，再判定出有一组邻边相等；先判定一个四边形是菱形，再判定出有一个角是直角才能得出正确答案．