题目内容
 (2012•丰润区一模)如图,已知⊙O的直径AB与弦CD相互垂直,垂足为点E,过点B作CD的平行线与弦AD的延长线相交于点F,且AD=3,cos∠BCD=
(2012•丰润区一模)如图,已知⊙O的直径AB与弦CD相互垂直,垂足为点E,过点B作CD的平行线与弦AD的延长线相交于点F,且AD=3,cos∠BCD=| 3 | 4 |
(1)求证:BF为⊙O的切线.
(2)求⊙O的半径.
分析:(1)由AB⊥CD,BF∥CD,可得AB⊥BF,又由AB是⊙O的直径,即可证得BF为⊙O的切线;
(2)首先连接BD,由AB是⊙O的直径,可得∠ADB是直角,又由AD=3,cos∠BCD=
,即可得cos∠BAD=
=
,继而求得答案.
(2)首先连接BD,由AB是⊙O的直径,可得∠ADB是直角,又由AD=3,cos∠BCD=
| 3 |
| 4 |
| AD |
| AB |
| 3 |
| 4 |
解答: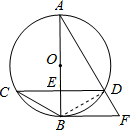 (1)证明:∵AB⊥CD,BF∥CD,
(1)证明:∵AB⊥CD,BF∥CD,
∴AB⊥BF,
∵AB是⊙O的直径,
∴BF为⊙O的切线;
(2)解:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠BCD=∠BAD,cos∠BCD=
,
∴cos∠BAD=
=
,
∵AD=3,
∴AB=4,
∴⊙O的半径为2.
 (1)证明:∵AB⊥CD,BF∥CD,
(1)证明:∵AB⊥CD,BF∥CD,∴AB⊥BF,
∵AB是⊙O的直径,
∴BF为⊙O的切线;
(2)解:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠BCD=∠BAD,cos∠BCD=
| 3 |
| 4 |
∴cos∠BAD=
| AD |
| AB |
| 3 |
| 4 |
∵AD=3,
∴AB=4,
∴⊙O的半径为2.
点评:此题考查了切线的判定、圆周角定理以及锐角三角函数的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与转化思想的应用.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 (2012•丰润区一模)在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则CF:CA=( )
(2012•丰润区一模)在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则CF:CA=( )