题目内容
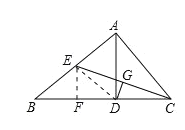
【题目】在![]() 中,AD是BC边上高线,E是AB的中点,
中,AD是BC边上高线,E是AB的中点,![]() 于G,
于G,![]() .
.

(1)求证:![]()
(2)若![]() ,求CE的长.
,求CE的长.
【答案】(1)证明见详解;(2)![]() .
.
【解析】
(1)连接DE,由直角三角形斜边上的中线等于斜边上的一半,可得:DE=AE=BE,从而得到CD=DE,根据等腰三角形三线合一,即可得证;
(2)作EF⊥BD于点F,根据勾股定理,可得:AB=10,即BE=5,由BE=DE,EF⊥BD,
得到:BF=DF=![]() BD=4,进而得到:
BD=4,进而得到:![]() ,最后在RtCEF中,利用勾股定理,即可求解.
,最后在RtCEF中,利用勾股定理,即可求解.
(1)连接DE,
∵AD是BC上的的高,
∴∠ADB=90°,
∵CE是AB边上的中线,
∴DE=AE=BE,
∵CD=AE,
∴CD=DE,
即CDE是等腰三角形,
∵DG⊥CE,
∴CG=GE(等腰三角形三线合一);
(2)作EF⊥BD于点F,
∵AD=6,BD=8,
∴AB=![]() ,
,
∴BE=5,
∵BE=DE,EF⊥BD,
∴BF=DF=![]() BD=4,
BD=4,
∵![]() ,
,
∴![]() ,
,
∵CD=DE=BE=5,
∴CF=DF+CD=4+5=9,
在RtCEF中,∠CFE=90°,EF=3,CF=9,
∴![]() .
.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目