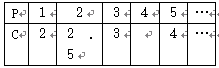
��Ŀ����
��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��l1��x���ڵ㣨1��0����ֱ��l2��x���ڵ㣨2��0����ֱ��l3��x���ڵ㣨3��0����ֱ��ln��x���ڵ㣨n��0��������y=x��ͼ����ֱ��l1��l2��l3����ln�ֱ��ڵ�A1��A2��A3����An������y=2x��ͼ����ֱ��l1��l2��l3����ln�ֱ��ڵ�B1��B2��B3����Bn�������OA1B1�������ΪS1���ı���A1A2B2B1���������S2���ı���A2A3B3B2���������S3�����ı���An-1AnBnBn-1���������Sn����ôS2011= ��


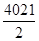
����������������⣬An-1Bn-1=2��n-1��-��n-1��=2n-2-n+1=n-1��
AnBn=2n-n=n��
��ֱ��ln-1��x���ڵ㣨n-1��0����ֱ��ln��x���ڵ㣨n��0����
��An-1Bn-1��AnBn����ln-1��ln��ľ���Ϊ1��
���ı���An-1AnBn Bn-1�����Σ�
Sn=
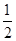 ��n-1+n����1=
��n-1+n����1=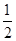 ��2n-1����
��2n-1������n=2011ʱ��S2011=
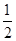 ��2��2011-1��=
��2��2011-1��=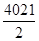 ��
���������������⣬����ֱ�߽���ʽ���An-1Bn-1��AnBn��ֵ�ǽ���Ĺؼ���Ҫע�����Ķ�Ӧ��ϵ����Ҳ�DZ��������׳����ĵط���

��ϰ��ϵ�д�
 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
�����Ŀ
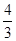 x��ͼ���ڵ�A������x�ύ�ڵ�B.
x��ͼ���ڵ�A������x�ύ�ڵ�B.
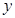 (Ԫ)��ӡ������
(Ԫ)��ӡ������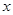 (��)֮��Ĺ�ϵʽ��
(��)֮��Ĺ�ϵʽ��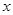 �ύ�ڵ�C����
�ύ�ڵ�C����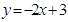 ��ͼ���ϣ� ��
��ͼ���ϣ� �� ,���ÿ����1km,�����½�3
,���ÿ����1km,�����½�3