题目内容
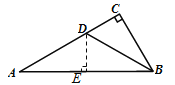
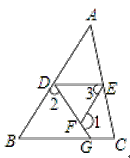
【题目】如图,已知△ABC中,AB=AC,D为BC边的中点,BE平分∠ABC,交AD于E,F为△ABC外一点,且∠ACF=![]() ∠ACB,BE=CF,
∠ACB,BE=CF,
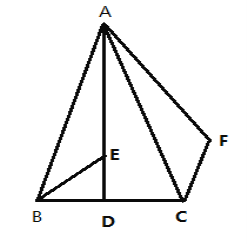
(1)求证:∠BAF=3∠BAD
(2)若DE=5,AE=13,求线段AB的长.
【答案】(1)详见解析;(2)19.5.
【解析】
(1)由角平分线得∠ABE=∠ACF,证明△ABE≌△ACF(SAS)得∠BAE=∠CAF,根据三线合一性质得∠BAE=∠DAC=∠CAF,即可解题,
(2)根据角平分线性质得DE=EH=5,在Rt△AEH中,勾股定理得AH=12, 设BD=BH=a在Rt△ABD中,勾股定理求BH=7.5,即可解题.
(1)![]() AB=AC
AB=AC
![]() ∠ABC=∠ACB
∠ABC=∠ACB
![]() BE平分∠ABC
BE平分∠ABC
![]() ∠ABE=
∠ABE=![]() ∠ABC
∠ABC
又![]() ∠ACF=
∠ACF=![]() ∠ACB
∠ACB
![]() ∠ABE=∠ACF
∠ABE=∠ACF
又![]() BE=CF
BE=CF
![]() △ABE≌△ACF
△ABE≌△ACF
∴∠BAE=∠CAF
![]() AB=AC,D为BC中点
AB=AC,D为BC中点
![]() ∠BAD=∠CAD
∠BAD=∠CAD
∴∠BAF=3∠BAD
(2)过E作EH⊥AB于H
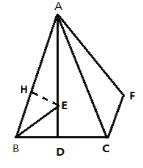
![]() AB=AC,D为BC中点
AB=AC,D为BC中点
![]() AD⊥BC
AD⊥BC
![]() BE平分∠ABC,
BE平分∠ABC,
∴DE=EH=5
∴Rt△AEH中,AH=![]()
![]() ∠BHE=∠BDE=90°,DE=EH,BE=BE
∠BHE=∠BDE=90°,DE=EH,BE=BE
![]() △BDE≌△BEH
△BDE≌△BEH
![]() BD=BH
BD=BH
设BD=BH=a
则Rt△ABD中,![]()
![]()
![]()
解得a=7.5
![]() AB=AH+BH=7.5+12=19.5
AB=AH+BH=7.5+12=19.5

【题目】某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
销售额(万元) | 17 | 19 | 20 | 21 | 25 | 26 | 28 | 30 |
频数(人数) | 1 | 1 | 3 | 3 |
(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.
【题目】阅读下列材料: 某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
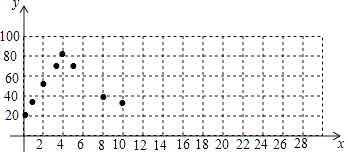
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
接通电源后的时间x | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
水箱中水的温度y | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
m的值为;
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式; 当4<x≤16时,写出一个符合表中数据的函数解析式;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源min.