Question

【题目】如图，在Rt△ABC中，BC=2，∠BAC=30°，斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动，下列结论：
①若C、O两点关于AB对称，则OA=2 ；
②C、O两点距离的最大值为4；
③若AB平分CO，则AB⊥CO；
④斜边AB的中点D运动路径的长为 ；
其中正确的是（把你认为正确结论的序号都填上）．

Answer 1

【答案】①②③
【解析】解：在Rt△ABC中，∵BC=2，∠BAC=30°，
∴AB=4，AC= =2 ，①若C、O两点关于AB对称，如图1，

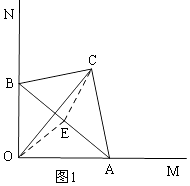
∴AB是OC的垂直平分线，
则OA=AC=2 ；
所以①正确；②如图1，取AB的中点为E，连接OE、CE，
∵∠AOB=∠ACB=90°，
∴OE=CE= AB=2，
当OC经过点E时，OC最大，
则C、O两点距离的最大值为4；
所以②正确；③如图2，同理取AB的中点E，则OE=CE，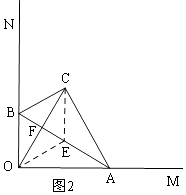

∵AB平分CO，
∴OF=CF，
∴AB⊥OC，
所以③正确；④如图3，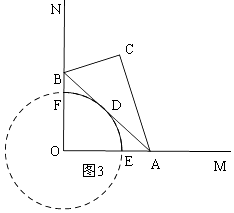

斜边AB的中点D运动路径是：以O为圆心，以2为半径的圆周的 ，
则： =π．
所以④不正确；
综上所述，本题正确的有：①②③；
所以答案是：①②③．
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识，掌握在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．