题目内容
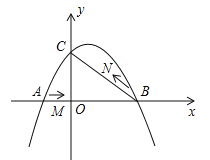
【题目】如图，在平面直角坐标系中，抛物线
（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B坐标为（4，0），抛物线的对称轴方程为x=1．
（1）求抛物线的解析式；
（2）点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN的面积为S，点M运动时间为t，试求S与t的函数关系，并求S的最大值；
（3）在点M运动过程中，是否存在某一时刻t，使△MBN为直角三角形？若存在，求出t值；若不存在，请说明理由．
【答案】（1）
；（2）S=
，运动1秒使△PBQ的面积最大，最大面积是
；（3）t=
或t=
．
【解析】
试题分析：（1）把点A、B、C的坐标分别代入抛物线解析式，列出关于系数a、b、c的解析式，通过解方程组求得它们的值；
（2）设运动时间为t秒．利用三角形的面积公式列出S△MBN与t的函数关系式．利用二次函数的图象性质进行解答；
（3）根据余弦函数，可得关于t的方程，解方程，可得答案．
试题解析：（1）∵点B坐标为（4，0），抛物线的对称轴方程为x=1，∴A（﹣2，0），把点A（﹣2，0）、B（4，0）、点C（0，3），分别代入
（a≠0），得：
，解得：
，所以该抛物线的解析式为：；
（2）设运动时间为t秒，则AM=3t，BN=t，∴MB=6﹣3t．由题意得，点C的坐标为（0，3）．在Rt△BOC中，BC=
=5．如图1，过点N作NH⊥AB于点H，∴NH∥CO，∴△BHN∽△BOC，∴
，即
，∴HN=
t，∴S△MBN=
MBHN=（6﹣3t）t，即S= =
，当△PBQ存在时，0＜t＜2，∴当t=1时，S△PBQ最大=．
答：运动1秒使△PBQ的面积最大，最大面积是；
（3）如图2，在Rt△OBC中，cos∠B=
．
设运动时间为t秒，则AM=3t，BN=t，∴MB=6﹣3t．
①当∠MNB=90°时，cos∠B=
，即
，化简，得17t=24，解得t=；
②当∠BMN=90°时，cos∠B=
，化简，得19t=30，解得t=．
综上所述：t=或t=时，△MBN为直角三角形．
