题目内容
 如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过点D作EF∥BC,EF交AB于E,交AC于F,判断线段EF和BE、CF的关系,并写出理由.
如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过点D作EF∥BC,EF交AB于E,交AC于F,判断线段EF和BE、CF的关系,并写出理由.考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:由△ABC中,∠ABC、∠ACB的平分线相交于点D,过点D作EF∥BC,易得△BED与△CDF是等腰三角形,继而证得结论.
解答:解:EF=BE+CF.
理由:∵∠ABC、∠ACB的平分线相交于点D,
∴∠ABD=∠DBC,∠ACD=∠DCB,
∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠BCD,
∴∠ABD=∠EDB,∠ACD=∠FDC,
∴BE=DE,DF=CF,
∴EF=DE+DF=BE+CF.
理由:∵∠ABC、∠ACB的平分线相交于点D,
∴∠ABD=∠DBC,∠ACD=∠DCB,
∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠BCD,
∴∠ABD=∠EDB,∠ACD=∠FDC,
∴BE=DE,DF=CF,
∴EF=DE+DF=BE+CF.
点评:此题考查了等腰三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
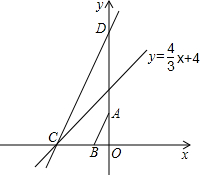 如图,在平面直角坐标系中,直线CD交x轴、y轴于点C、D,点B在x轴上,且点B、C到坐标原点O的距离的比为1:3,点D在y轴上,且AD的长为7,若tan∠OCD=3,sin∠ABO=
如图,在平面直角坐标系中,直线CD交x轴、y轴于点C、D,点B在x轴上,且点B、C到坐标原点O的距离的比为1:3,点D在y轴上,且AD的长为7,若tan∠OCD=3,sin∠ABO= 如图,已知△ABC中,AB=AC,D在BC上,E在AC上,且AD=AE,∠BAD=46°,那么∠CDE的度数为
如图,已知△ABC中,AB=AC,D在BC上,E在AC上,且AD=AE,∠BAD=46°,那么∠CDE的度数为