Question

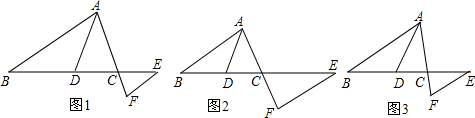
在△ABC中，已知AB＞AC，AD平分∠BAC交BC于点D，点E在DC的延长线上，且

DE

BD

=k，过E作EF∥AB交AC的延长线于F．
（1）如图1，当k=1时，求证：AF+EF=AB；
（2）如图2，当k=2时，直接写出线段AF、EF、AB之间满足的数量关系：

AF+EF=2AB

；
（3）如图3，当

DE

BD

=k时，请猜想线段AF、EF、AB之间满足的数量关系（含k），并证明你的结论．

Answer 1

分析：（1）延长AD、EF交于点G，当k=1时，DE=BD，再根据∠BDA=∠EDG，BD=ED，证出△ABD≌△GED，得出AB=GE，又因为∠BAD=∠DAC，所以∠FGD=∠DAC，AF=GF，
即可证出AF+EF=AB；
（2）当k=2时，同（1）可得△ABD∽△GED，根据相似三角形的对应边成比例即可得出结论；
（3）当

DE

BD

=k时，同（1）可得△ABD∽△GED，根据相似三角形的对应边成比例即可得出结论．

解答：（1）证明：如图1，延长AD、EF交于点G，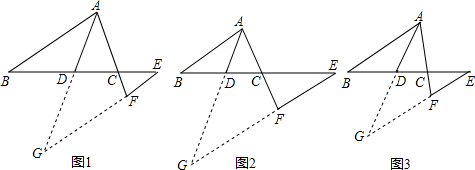
当k=1时，DE=BD
∵EF∥AB，
∴∠BAD=∠EGD，
在△ABD与△GED中，

∠BAD=∠EGD ∠BDA=∠EDC BD=ED

，
∴△ABD≌△GED（AAS），
∴AB=GE，
又∵AD平分∠BAC，
∴∠BAD=∠DAC，
∴∠FGD=∠DAC，
∴AF=GF，
∴AF+EF=AB；

（2）解：如图2，延长AD、EF交于点G，当k=2时，
∵EF∥AB，
∴∠BAD=∠EGD，
又∵∠BDA=∠EDG，
∴△ABD∽△GED，
∴

GE

AB

=

DE

BD

=2，即GE=2AB，
又∵AD平分∠BAC，
∴∠BAD=∠DAC，
∴∠FGD=∠DAC，
∴AF=GF，
∴AF+EF=2AB；

（3）猜想：AE+EF=kAB．
证明：如图3，延长AD、EF交于点G，当

DE

BD

=k时，
∵EF∥AB，
∴∠BAD=∠EGD，
又∵∠BDA=∠EDG，
∴△ABD∽△GED，
∴

GE

AB

=

DE

BD

=k，即GE=kAB，
又∵AD平分∠BAC，
∴∠BAD=∠DAC，
∴∠FGD=∠DAC，
∴AF=GF，
∴AF+EF=kAB．

点评：本题考查的是相似三角形综合题，根据题意作出辅助线，构造出相似三角形，再根据相似三角形的性质求解是解答此题的关键．